Resumo de fisica: Resistores - aprofundamento

Resistores - Simetria e problemas tridimensionais - aula 1

CHAVEAMENTO EM CIRCUITOS:

Diagrama, EsquemáticoDescrição gerada automaticamente

Para circuitos com chaves, analisar por onde passa sempre a corrente, como acima, que, quando a chave está fechada, temos quatro resistores R em paralelo, e com a chave aberta temos apenas um resistor R ligado ao gerador. Isso pode permitir controle de corrente e consumo, uma das aplicações do chaveamento.

FUNCIONAMENTO DE EQUIPAMENTOS EM LINHA DE TENSÃO ALTERNADA:

1. SE A TENSÃO NOMINAL FOR IGUAL À TENSÃO DE LINHA, TEMOS FUNCIONAMENTO E VIDA ÚTIL NOMINAIS E ESPERADOS.

2. SE A TENSÃO NOMINAL FOR MAIOR QUE A TENSÃO DE LINHA, TEMOS SUBFUNCIONAMENTO, COM MENOR DESEMPENHO E CONSUMO E VIDA ÚTIL MUITAS VEZES AUMENTADA.

3. SE A TENSÃO NOMINAL FOR MENOR QUE A TENSÃO DE LINHA, TEMOS SUPERFUNCIONAMENTO, COM MAIOR DESEMPENHO E CONSUMO, COM VIDA ÚTIL MUITAS VEZES DIMINUÍDA, E, EM ALGUNS CASOS, ‘QUEIMA DO EQUIPAMENTO’.

Resistores - Simetria e problemas tridimensionais - aula 2

PONTES DE WHEATSTONE:

são circuitos mistos tais que os pontos intermediários dos ramos são isopotenciais, isto é, a leitura da tensão entre eles é sempre zero, o que só pode ocorrer se o produto das resistências diagonalmente opostas for constante. Aí diz-se que a ponte está EQUILIBRADA.

pontes de wheatstone

Logo,
$R_1\cdot R_3=R_2\cdot R_4$ para $G=0$ ,
e as ddps de 1 e 4 são iguais,
as ddps de 2 e 3 são iguais também,
além das correntes em 1 e 2 são iguais
e as de 4 e 3 são iguais também.

Cuidado!!! O mais difícil às vezes é reconhecer as pontes...

CHAVES OU INTERRUPTORES: são elementos que cortam correntes em determinados pontos do circuito, de tal modo que quando estão fechadas, têm resistência nula e quando estão abertas, tem resistência infinita.

Resistores - Simetria e problemas tridimensionais - aula 3

CIRCUITOS TRIDIMENSIONAIS E COM SIMETRIAS ESPECIAIS:
1. EM ALGUNS CIRCUITOS PERCEBEMOS QUE UM PADRÃO SE REPETE INFINITAMENTE.
ESSE PADRÃO PODE GERAR O QUE CHAMAMOS DE PROCESSO APROXIMATIVO CONVERGENTE, ONDE, DEPOIS DE MUITAS OPERAÇÕES SEMELHANTES, MAIS UMA OU MENOS UMA NÃO VARIAM MUITO O RESULTADO DO QUAL ESTAMOS NOS APROXIMANDO.
VAMOS VER UM EXEMPLO:

O circuito acima é feito de várias repetições desde o começo, com 3 R em série, em paralelo com R e depois em série com 2 R, depois em paralelo com R, e assim indefinidamente. Logo, se fizermos mais uma interação, mais uma vez, o resultado não se altera, dando x novamente, logo faremos x em paralelo com R depois em série com 2 R e depois vamos igualar a x:
$\frac{x\cdot R}{x+R}+2\cdot R=x$ logo: $x\cdot R+2\cdot R\cdot(x+R)=x\cdot(x+R)$ e então: $x\cdot R+2\cdot R\cdot x+2R^2=x^2+x\cdot R$ o que nos leva a: $x^2-2Rx-2R^2=0$ o que nos leva a $R_{eq}=x=R\cdot(1+\sqrt{3})$ .
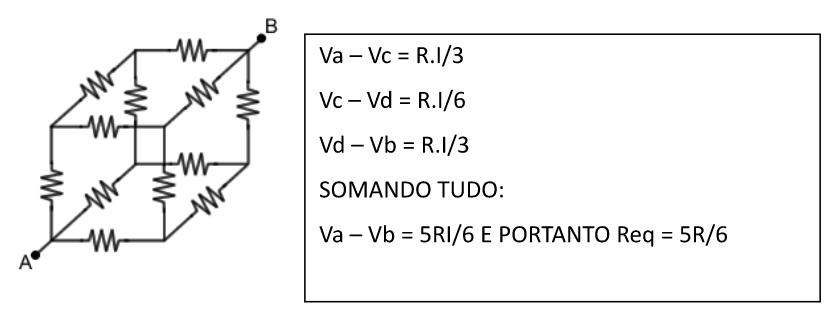
1. EM ALGUNS CIRCUITOS PERCEBEMOS A SIMETRIA E USAMOS O MÉTODO DA LINHA DE POTENCIAL, COMO NO CUBO ABAIXO ONDE TODOS OS RESISTORES VALEM R: