Resumo de fisica: Dilatação térmica I
DILATAÇÃO TÉRMICA, CASO ENDOTÉRMICO, OU DILATAÇÃO PROPRIAMENTE DITA:
- O corpo absorve calor do meio, aumentando a agitação das partículas, e, consequentemente o número médio de choques.
- COM O AUMENTO DO NÚMERO MÉDIO DE CHOQUES, A DISTÃNCIA MÉDIA ENTRE AS PARTÍCULAS AUMENTA, O QUE É PERCEBIDO MACROSCOPICAMENTE COMO AUMENTO OU DILATAÇÃO DE DIMENSÕES DO CORPO.
- CORPOS EM GERAL DILATAM MUITO POUCO, UMA PARTE EM CEM MIL, LOGO OS COEFICIENTES DE DILATAÇÃO TODOS GIRAM EM TORNO DE 10-5...
- SE O CORPO ESTÁ PERDENDO CALOR, DIZEMOS QUE TEMOS DILATAÇÃO NEGATIVA, OU CONTRAÇÃO, QUE É O CASO EXOTÉRMICO.
- As lâminas bimetálicas são muito usadas como chaves duais e elementos de termostatos que são controladores de potência. O que devemos guardar é que a lâmina sempre deflete e entorta para o lado e para o sentido do material mais rígido, portanto que menos dilata.
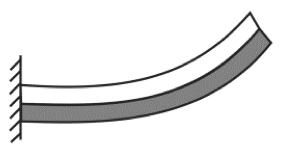
No caso acima temos aquecimento o material branco dilata menos, é mais rígido, e o material escuro dilata mais, é menos rígido, é mais maleável. No caso de resfriamento, o que dilata mais se contrai mais também e aí a lâmina deflete no sentido oposto.
DILATAÇÃO TÉRMICA: equações e gráficos relacionados:
A dilatação, que é o aumento da agitação, aumentando o número médio de choques e as dimensões macroscópicas do corpo.
A dilatação absoluta depende do comprimento inicial, do material e da variação de temperatura; a dilatação relativa linear só depende do material e da variação de temperatura, e temos também o comprimento final do corpo em função da temperatura, como mostram as equações abaixo:
Com comprimento inicial,
é o coeficiente de dilatação linear,
é a variação de temperatura e
a dilatação absoluta do corpo.
Para calcular a dilatação relativa temos que achar a variação de comprimento e dividir pelo comprimento inicial.
E o comprimento final, isolando L (comprimento final) na equação básica vale:
Para encaixe final das peças, quando houver duas peças, deve-se igualar os comprimentos finais.
DILATAÇÃO TÉRMICA: GRÁFICOS E DILATAÇÃO DO VAZIO:
Análise gráfica:
No gráfico do comprimento em função da temperatura, em sua aproximação linear, o coeficiente angular é numericamente igual ao coeficiente de dilatação linear vezes o comprimento inicial.
Para materiais com gráficos paralelos, significa que quanto mais o material for rígido, maior a peça e quanto menos for rígido, menor a peça, é assim em qualquer sistema estável termicamente, até em nós mesmos, onde os ossos muito rígidos ‘podem’ ser grandes e órgãos menores podem ser mais moles e maleáveis, como nossos órgãos internos.
DILATAÇÃO DE VAZIOS OU BURACOS OU OMISSÕES DE MATERIAL:
Os vazios, para que respeitem a potente segunda lei da termo, devem dilatar como se fossem cheios, como se fossem feitos do material circundante, mantendo as proporções da peça, supondo que não haja mudança de fase.
DILATAÇÃO TÉRMICA SUPERFICIAL:
Podemos adaptar a equação da dilatação linear para os processos areolares ou superficiais, como mostrado abaixo:
é a área inicial,
é o coeficiente de dilatação superficial, e
é a variação de temperatura.
Caso queiramos a área final:
EXEMPLOS de dilatação superficial: placas, chapas, tecidos, pele, camadas de tinta na parede, etc.
DILATAÇÃO TÉRMICA VOLUMÉTRICA e COEFICIENTES DE DILATAÇÃO:
A dilatação em três dimensões é a dilatação volumétrica.
Na verdade, a dilatação volumétrica é a única que ocorre, pois temos objetos espaciais no mundo, porém, algumas vezes, uma ou duas dimensões são desprezíveis gerando dilatações desprezíveis, e é aí que surgem as dilatações aproximadas superficial e linear.
A dedução da equação principal:
Logo, desprezando os termos muito pequenos:
Ou para a dilatação absoluta:
E os coeficientes se relacionam segunda a relação abaixo:






