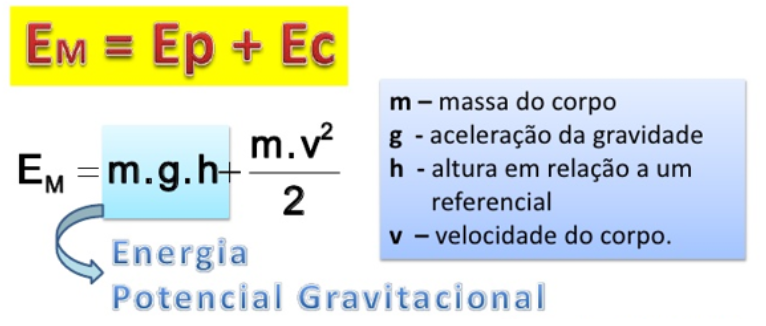
Resumo de fisica: Energia

Energia cinética e Teorema da energia cinética

A energia cinética de um corpo de massa m, para baixas velocidades, é a energia de movimento, que é dada por:

$E_c=\frac{m\cdot v^2}{2}$
com m sendo a massa do corpo e v a velocidade instantânea do corpo.
Teorema da energia cinética, que liga o trabalho da força resultante com a variação da energia cinética, também é chamado teorema da força resultante, que diz que o trabalho da força resultante é igual à variação da energia cinética do corpo:

$\tau =F\cdot \Delta S$

$\tau =m\cdot\left ( \frac{V^2_F-V^2_0}{2\Delta S} \right ) \Delta S$

$\tau =m\cdot\left ( \frac{V^2_F-V^2_0}{2} \right )$

Ou seja, isolando o deslocamento na equação de Torricelli e substituindo na própria definição de trabalho, encontramos que o trabalho resultante é a variação da energia cinética

$\tau =\Delta E_c=\frac{m\cdot v_f^2}{2}-\frac{m\cdot v_i^2}{2}$

Se partir do repouso a velocidade inicial é nula, e se parar no final a velocidade final é nula, e se a velocidade for constante o trabalho resultante é nulo.

Energia - Forças conservativas e Teoremas

O trabalho das forças conservativas é igual a menos a variação de energia potencial. As forças conservativas são aquelas cujo trabalho associado às mesmas não depende do percurso e da trajetória:

Foto em preto e brancoDescrição gerada automaticamente DiagramaDescrição gerada automaticamente

Os trabalhos das forças conservativas são iguais em cada um dos exemplos, já que não dependem do caminho. Isso ocorre com a força gravitacional, a força elétrica e a força elástica: os trabalhos ou as energias trocadas não dependem do percurso, só do nível inicial e do nível final de energia:

$T_{FD}=-\Delta E_P$

Ou seja, o trabalho da força conservativa é a energia potencial inicial menos a final

Energia potencial gravitacional e Energia potencial elástica

A energia gravitacional é o potencial gravitacional vezes a massa de prova ou massa orbitando, logo, temos:

$E_{pg}=V_{pg}\cdot m=-\frac{G\cdot M\cdot m}{d}$

onde $d=R+h$

Onde $R$ é o raio do planeta ou corpo central e $h$ é a altitude em relação à sua superfície. Se multiplicarmos em cima e em baixo por d e pensarmos que a profundidade (que se mede de cima para baixo) de qualquer coisa é menos a sua altura (que se mede de baixo para cima), temos:

$E_{pg}=V_{pg}\cdot m=-\frac{G\cdot M\cdot m}{d^2}$

Esta relação é válida quando temos gravidade aproximadamente constante, isto é, variações de altura muito pequenas.

A energia potencial elástica é a área do gráfico da força elástica pela deformação, que é a variação do comprimento da mola, já que a força elástica não é constante ao longo da distância:

CONDIGITAL

$E_{Pel}=\frac{k\cdot X^2}{2}$

Teorema da energia mecânica

Teorema das forças não conservativas, ou teorema da energia mecânica, que diz que o trabalho dos atritos é igual à variação da energia mecânica total do corpo...

Uma imagem contendo DiagramaDescrição gerada automaticamente

Ou seja, o trabalho da força de atrito, que representa a energia dissipada por fricção, é igual à variação da energia mecânica total em cada ponto.

Ou seja, podemos dizer que a perda de energia de um sistema é o trabalho do atrito e das forças resistivas não conservativas que é igual à variação da energia mecânica no trecho.

Lembrar também:
a) Que o trabalho do atrito, em superfícies horizontais, é a normal vezes o coeficiente de atrito vezes a distância ou deslocamento
b) As forças não conservativas não são apenas os atritos, podem ser forças como tração ou outra qualquer, o atrito é apenas o caso mais comum.

Sistema mecânico conservativo

Quando um ou mais corpos estão sujeitos a forças conservativas, ou seja, forças que podem armazenar energia e torná-la totalmente útil de forma reversível

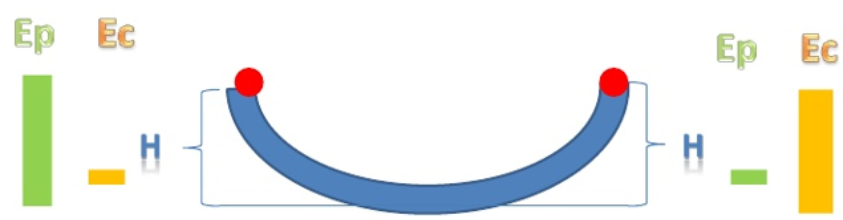
Como acima, no ‘half’ de skate: nos pontos vermelhos a energia potencial gravitacional é máxima e no ponto mais baixo a energia cinética é mais alta, mas a mecânica total em todos os pontos é a mesma.

A energia mecânica se conserva quando a energia potencial $(E_p)$ transforma-se integralmente em energia cinética: