Resumo de fisica: Cinemática Vetorial - Parábola de Segurança - aprofundamento

Lançamento Oblíquo - Parábola de segurança - aula 1

Sabemos que o alcance máximo dos máximos, que ocorre a 45º, vale, para a horizontal, $x=\frac{v_0^2}{g}$ e este ponto será a raiz positiva de nossa parábola envoltória. A outra raiz é o mesmo valor só que negativo.
Sabemos também que a máxima altura das máximas ocorre quando temos ângulo de lançamento igual a 90º, e vale $y=H=\frac{v_0^2}{2\cdot g}$ , que será o intercepto vertical ou coeficiente linear da parábola, quando x = 0. Como temos o vértice pertencente ao eixo vertical, o coeficiente b da parábola é nulo e temos:

$y=ax^2+bx+c$ , com $b=0$ ,
mas para $x=0$ , $y=c=\frac{v_0^2}{2\cdot g}$ ;
e para $x=\pm \frac{v_0^2}{g}$ , $y=0$ ,
logo $a=\frac{-g}{2\cdot v^2_0}$ o que resulta na equação geral dada por:

DiagramaDescrição gerada automaticamente

Essa equação permite descobrir a velocidade de lançamento tendo as coordenadas do alvo e também testar os possíveis ângulos de tiro.

Lançamento Oblíquo - Parábola de segurança - aula 2

A Parábola de Segurança: Parábola de Segurança

A parábola de segurança é a parábola envoltória de todas as parábolas possíveis para uma dada velocidade v0. Vamos tomar a equação da trajetória e desenvolvê-la mais para podermos estudar os ângulos de tiro.
Mas é importante saber que a zona de risco, geralmente interna, é válida para tiros, projéteis e obus agressivos e a zona de segurança é a externa, onde o corpo não pode mais ser atingido por nenhum desses obuses.
Mas numa missão de paz, de ajudar comunidades com alimentos e doações, reparar que as zonas se invertem: a interna é a boa, de segurança, onde o ser humano pode ser atingido pelos alimentos e doações e a zona de fora é a de risco, onde nenhum alimento pode atingir as pessoas.
EQUAÇÕES RELACIONADAS:
EQUAÇÃO GENERALIZADA DAS POSSÍVEIS TRAJETÓRIAS, PARA VELOCIDADE INICIAL E GRAVIDADE CONSTANTES:

$y=(tg(\theta_0 ))x-\frac{g\cdot x^2}{2\cdot v^2_0\cdot(cos^2(\theta_0 ))}$

Lançamento Oblíquo - Parábola de segurança - aula 3

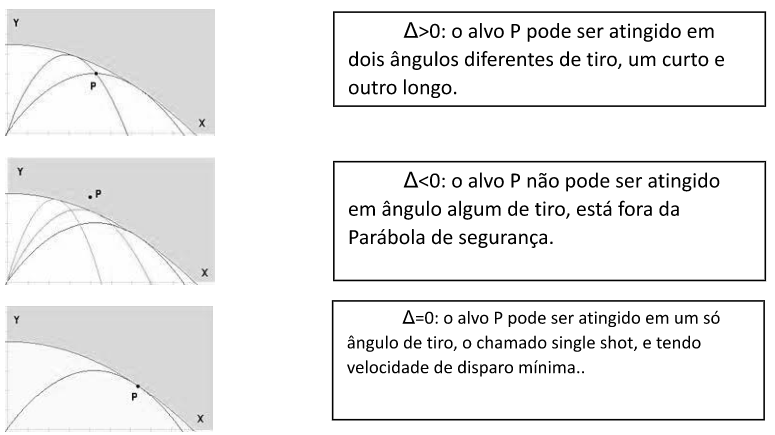
ÂNGULOS DE TIRO POSSÍVEIS:

A parábola de segurança é a parábola envoltória de todas as parábolas possíveis para uma dada velocidade v0. Vamos tomar a equação da trajetória e desenvolvê-la mais para podermos estudar os ângulos de tiro.
Analisemos a equação generalizada das possíveis trajetórias, para velocidade de lançamento e gravidade constantes, com ângulo de lançamento igual a θ ou α em relação à horizontal.
$y=(tg(\theta_0 ))x-\frac{g\cdot x^2}{2\cdot v^2_0\cdot(cos^2(\theta_0 ))}$ , mas o inverso de cos ao quadrado é secante ao quadrado!!
mas Relações fundamentais - Alfaconnection logo temos:

$y=(tg(\theta_0 ))x-\frac{g\cdot x^2}{2\cdot v^2_0\cdot(sec(2\theta_0 ))}$ o que dá:

e resolvendo a equação de segundo grau para tangente do ângulo de lançamento, temos, estudando os deltas possíveis: