Resumo de fisica: Movimento Circular: Equações

Grandezas angulares e movimento circular uniforme - Exemplos

MCU: PROBLEMAS DE ENCONTROS ENTRE DOIS MÓVEIS:
Um dos problemas mais clássicos de MCU é aquele que, dados dois pontos que desenvolvem movimento circular uniforme, portanto com velocidades angulares, frequência e período constantes para cada um deles, pede o instante e às vezes a posição angular onde os dois pontos se encontram pela primeira vez, ou quando eles voltam a se encontrar no mesmo ponto de partida. Lembrar também que a aceleração tangencial é nula, pelo fato de que a Fcp associada ao MCU é perpendicular ao movimento e não realiza trabalho para raio R constante.
Os dois pontos podem ou não sair do mesmo ponto, e o caso mais clássico, que é o que vamos analisar, eles efetivamente saem da mesma posição angular ou fase. Quando isso ocorre um dos jeitos de resolver é usar a teoria do movimento relativo, isto é, colocamos o referencial em um dos corpos, como se ele estivesse parado, e calculamos as velocidades lineares e angulares relativas, que nada mais são do que o deslocamento relativo pelo intervalo de tempo, suposto absoluto, portanto invariante considerando energias cinéticas baixas:

$\omega_{rel}=\omega _2\pm \omega _1=\frac{\Delta \theta _{rel}}{\Delta t}=\frac{n\cdot 2 \cdot\pi \cdot R}{\Delta t}$

Com ω: velocidades angulares de 1 e 2 e a relativa, que é sempre a subtração das duas, segundo o teorema de Galileu. O deslocamento angular relativo, $\Delta \theta _{rel}$ , é também a subtração vetorial dos deslocamentos de 1 e 2, MAS TAMBÉM É $n\cdot 2 \cdot\pi \cdot R$ isto é, n é a ordem do encontro e R é o raio de curvatura do MCU desenvolvido. Para n=1, calcularemos o tempo do primeiro encontro ou o tempo entre dois encontros consecutivos quaisquer; para n=3 temos o tempo do terceiro encontro, e assim por diante, o deslocamento representa ‘quantas voltas o mais rápido coloca sobre o mais lento, o retardatário’.
Se as velocidades estão para o mesmo sentido a relativa é a subtração da maior menos a menor velocidade;
Se as velocidades estão para sentidos opostos a relativa é a soma das duas, na verdade é uma menos menos a outra, já que a outra tem que ser negativa por ser oposta: VETORES OPOSTOS, SINAIS OPOSTOS.

Interface gráfica do usuário

Descrição gerada automaticamente com confiança média

Movimento circular uniforme - Transmissão de Movimentos

MCU: TRANSMISSÃO DE MCU: diferenciais, associação de polias com correias ou associação de engrenagens no mesmo eixo ou em eixos diferentes (coaxiais ou não coaxiais)

Os dois tipos de acoplamento:

No acoplamento com eixo comum, a velocidade angular, período, frequência são sempre iguais, e a velocidade periférica é tanto maior quanto maior for o raio;

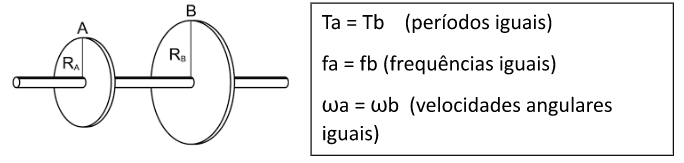
No acoplamento com eixos independentes, a velocidade linear é a mesma, isto é, o produto entre o raio da polia e a frequência é constante: a menor gira mais rápido (marcha leve) e a maior gira mais lentamente (marcha pesada):

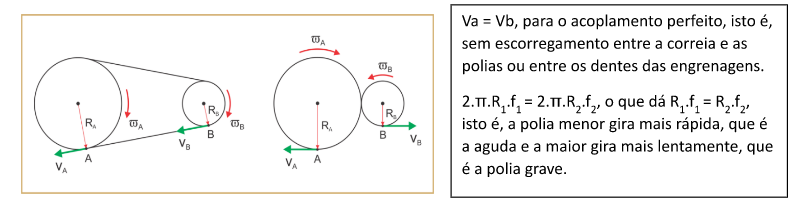
NA BICICLETA:
Lembrar que, para um aclive, uma subida, marcha leve pois a trajetória é pesada, isto é, coroa (onde fica o pedal) é pequena e catraca (onde fica a roda traseira) maior.
No declive, uma descida, marcha pesada pois a trajetória leve, isto é, coroa grande e catraca pequena. Quanto menor o raio da coroa, menor o torque e menores as forças exercidas, apesar das velocidades rotacionais serem maiores.....

Resultado de imagem para acoplamento entre polias MCU – Movimento Circular Uniforme

De A para B temos que a frequência é inversamente proporcional ao raio da polia e de B para R temos mesma frequência, período e velocidade angular.

Movimento circular uniformemente variado

O MCU, movimento circular uniforme só possui aceleração centrípeta, ligada à força resultante centrípeta, que serve para alterar SOMENTE a direção da velocidade tangencial instantânea, sem realizar trabalho ou mudar a energia cinética.

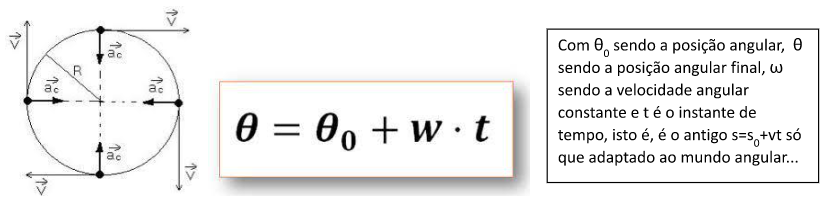
O MCUV, movimento circular uniformemente variado possui duas acelerações, a tangencial, que é paralela ao movimento e, portanto, realiza trabalho, isto é, altera a energia cinética da partícula, e a centrípeta, semelhante ao MCU, isto é, só muda a direção da velocidade, não alterando a energia cinética da partícula.

As equações utilizadas no MCUV são semelhantes àquelas aprendidas na cinemática linear, apenas trocando o espaço pelo ângulo, a velocidade tangencial pela angular, a aceleração tangencial pela aceleração média angular, como podemos ver nas relações tradicionais abaixo:

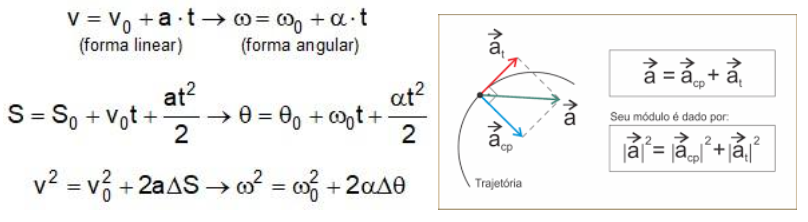
E não esqueçamos da propriedade da velocidade angular média:
$\omega _{rel}=\omega _1+\frac{\omega _2}{2}=\frac{\Delta \theta }{\Delta t}$ , isto é, a velocidade média angular é a média das velocidades angulares, além de ser, como em qualquer movimento circular, o deslocamento angular sobre o intervalo de tempo. E lembrar também que, se precisar passar o deslocamento angular para voltas, basta fazer $\Delta \theta =n\cdot 2 \cdot\pi$ , com n sendo o número de voltas dado no caso específico.

Movimento circular uniformemente variado - Equações e Exemplos

Ou seja, um ventilador, por exemplo que foi desligado, e é perguntado o número de voltas que os rotores terão que dar até o equipamento parar definitivamente. O que devemos fazer é descobrir é a velocidade angular inicial instantânea, a velocidade angular final instantânea, que será zero no caso pois o ventilador vai parar no final. De posse do tempo que demorou para parar, temos como calcular o número de voltas. Veja: supondo $\omega _0 = 4\cdot \pi \, rad/s$ , ω = 0 e o tempo de parada 20 s, temos a aplicação da velocidade angular média:
$\omega _1+\frac{\omega _2}{2}=\frac{\Delta \theta }{\Delta t}$ , logo $\frac{4\cdot \pi+0}{2}=\frac{\Delta\omega}{20}$ o que dá $\Delta\theta=40\cdot\pi\,rad$ E, para saber o número de voltas dadas até parar: $\Delta\theta=n\cdot2\cdot\pi$ logo: $40\cdot \pi=n\cdot2\cdot\pi$ , logo temos que n = 20 voltas até parar.