Resumo de fisica: Leis de Newton e Lei de Hooke II

Dinâmica - Lei de Hooke

Para fios ideais, a massa é muito menor que a massa dos objetos carregados, isto é, a força resultante em fios ideais é sempre nula, pois sua massa é desprezível, o que implica que as forças opostas em suas pontas sejam iguais. No nó o conceito de ângulo complementar nesse caso é importante.

Resultado de imagem para fios ideais

$F=-k\Delta x$

A lei de Hooke, de Robert Hooke (1678), diz que a força elástica em objetos elásticos é proporcional à deformação (Δx) na medida de uma constante da mola que é chamada de constante elástica da mola, k. O sinal de menos indica que a força elástica tem natureza restauradora, isto é, é sempre oposta ao vetor posição instantânea, e sempre aponta para o ponto de equilíbrio estático estável, onde a mola está em seu estado natural, sem energia e força.

Dinâmica - Lei de Hooke - Análise Gráfica

A força elástica é proporcional à deformação do corpo no regime elástico na medida da constante da mola, o que acaba gerando um gráfico retilíneo, crescente, a partir da origem, linear no período elástico e exponencial radicial no período plástico:

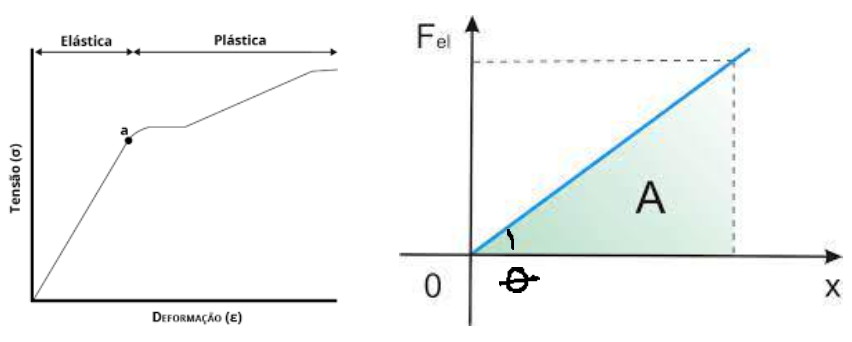
Propriedades do gráfico da força elástica:
A inclinação da função é numericamente igual à constante da mola: k = tgθ
A área do gráfico da força elástica pela deformação representa a energia elástica acumulada até tal deformação x.

Diagrama, Esquemático

Descrição gerada automaticamente

$E_{Pel}=\frac{k\cdot x^2}{2}$

Na fase plástica o material escoa, perde a linearidade, e não retorna basicamente às suas condições e dimensões iniciais.

Dinâmica - Lei de Hooke - Associação de Molas - Série e Paralelo

Diagrama, EsquemáticoDescrição gerada automaticamente

A deformação é a soma das deformações:

$X_{eq }= X_1 + X_2$

A força é constante, logo:

$K_{eq}=\frac{K_1\cdot K_2}{K_1+ K_2}$

Em paralelo:
A deformação é constante para as molas, sendo desprezadas as rotações
A força total é a soma das forças, logo:

$K_{eq }= K_1 + K_2$

Dinâmica - Dinâmica do Movimento Circular

FORÇAS RESULTANTES CENTRÍPETAS:
LEMBRAR QUE Fcp NÃO É TIPO DE FORÇA, E SIM RESULTANTE DE FORÇAS RADIAIS.
TIPOS DE FORÇA: PESO, TRAÇÃO, CONTATO (ATRITO E NORMAL) E FORÇA ELÁSTICA;
TIPOS DE RESULTANTE:

1.TANGENCIAL, QUE REALIZA TRABALHO E ALTERA O MÓDULO DE V E QUE É CALCULADA POR $F_{tg}=m\cdot a_{tg}=\frac{m\cdot\Delta V }{\Delta t}$ E:

2. CENTRÍPETA, QUE NÃO REALIZA TRABALHO, ALTERA A DIREÇÃO DA VELOCIDADE E QUE É CALCULADA POR:

$F_{cp} = \frac{m\cdot v^2}{R} = m\cdot\omega \cdot2\cdot R = m\cdot v\cdot \omega = \sum f\, para \,dentro - \sum f\, para\, fora$ ,
com resultante para dentro sempre maior que a resultante radial para fora, para que ocorra o movimento curvo de forma satisfatória.
Em lombadas, N menor que P e Fcp para baixo;
em valetas, N maior que P e Fcp para cima;
em globos da morte, no ponto mais alto, no ponto de descolamento, quando a normal tende a zero, a velocidade é crítica e mínima e vale √R.g, com o corpo em órbita;
em lombadas, a velocidade crítica é máxima, e tem o mesmo valor que a do item anterior.