Resumo de matematica: Probabilidade II

Adição de probabilidades

PROBABILIDADE DA UNIÃO DE EVENTOS

A probabilidade de ocorrer o evento $A$ ou o evento $B$ é dada pela soma da probabilidade de $A$ com a de $B$ , menos a probabilidade simultânea de $A$ e $B$ .

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Exemplo
No lançamento de um dado comum, qual a probabilidade de se obter um número ímpar ou maior que 4?

Probabilidade de $A\cup B$ : (número ímpar ou maior que 4)

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

$P(A\cup B)=\frac{3}{6}+\frac{2}{6}-\frac{1}{6}=\frac{4}{6}=\frac{2}{3}$

Atenção
Se dois eventos $A$ e $B$ são mutuamente exclusivos, a probabilidade de ocorrer $A$ ou $B$ é, simplesmente, a soma da probabilidade de $A$ com a probabilidade de $B$ , ou seja, $P(A\cup B)=P(A)+P(B)$ .

Exemplo: Se uma carta é selecionada aleatoriamente de um baralho comum, qual a probabilidade de ser um rei ou uma dama?

$P(rei\, ou\, dama)=P(rei)+P(dama)$

$P(rei\, ou\, dama)=\frac{4}{52}+\frac{4}{52}=\frac{8}{52}=\frac{2}{13}$

Observação

Pode-se provar que, para três eventos $A$ , $B$ e $C$ , a regra da soma de probabilidades é dada por:

$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)- P(B\cap C)+P(A\cap B\cap C)$

Adição de probabilidades - Outros exemplos

PROBABILIDADE DA UNIÃO DE EVENTOS

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Atenção

Se $A\cap B=\varnothing$ , dizemos que $A$ e $B$ são mutuamente exclusivos. Sendo $A\cap B=\varnothing$ e, portanto, $P(A\cap B)=0$ , temos que: $P(A\cup B)=P(A)+P(B)$

OBS 1: A definição se o problema trata de uma situação onde ocorre eventos simultâneos ou não deve acontecer durante a leitura e interpretação. Vale a pena lembrar que o conectivo “ou” será observado no problema como o motivador para o uso da relação acima.

OBS 2: É importante perceber que o conectivo “ou” muitas vezes não aparece de maneira explicita, mas numa leitura de possibilidades.

OBS 3: Resultados importantes

$C^0_n=1, \,\forall \,n\,\epsilon \,\mathbb{N}$
$C^1_n=n, \,\forall \,n\,\epsilon \,\mathbb{N}^*$
$C^n_n=1, \,\forall \,n\,\epsilon \,\mathbb{N}$
$C^n_{n-1}=n, \,\forall \,n\,\epsilon \,\mathbb{N}$

Probabilidade condicional

A probabilidade do evento $A$ , dada a ocorrência do evento $B$ , representada por $P(A/B)$ , é a probabilidade de ocorrer $A$ e $B$ dividida pela probabilidade do evento $B$ .

$P(A/B)=\frac{n(A\cap B)}{n(B)}$ $P(A/B)=\frac{n(A\cap B)}{n(B)}, n(B)\neq 0$

É importante perceber que, em P(A / B), o cálculo refere-se à probabilidade de A na certeza da ocorrência do evento B. Assim, o evento B é certo, enquanto que o evento A é incerto.

Observações
1. Analogicamente, a probabilidade do evento B, dada pela ocorrência do evento A, é dada por:

PBA=nA∩BnA , n(A)≠0

2. Em geral, P(A / B) não é igual a P(B / A). Isso ocorre porque, apesar de ambas as probabilidades condicionais apresentarem o mesmo numerador, cada uma delas pode ter um denominador diferente, já que a informação conhecida não é a mesma.

Exemplo
A probabilidade de um pescador sair para pescar é de 30% em dias de chuva e de 80% nos demais dias. Se, onde ele mora, a probabilidade de chuva num dia qualquer é de 40%.
Qual a probabilidade de chover em um dia em que o pescador foi pescar?

A probabilidade de chover em um dia em que o pescador foi pescar será representada por P(Chuva/Pesca). Observe que, nesse caso, temos uma probabilidade condicional, pois P(Chuva/Pesca) é a probabilidade de ocorrer chuva sabendo-se que o pescador foi pescar. Usando a relação da probabilidade condicional, temos:

PChuva|Pesca=n(Chuva e Pesca)n(Pesca)

PChuva|Pesca= 1260

PChuva|Pesca= 15=20%

PChuva|Pesca=20%

Probabilidade condicional - Outros exemplos

A probabilidade do evento $A$ , dada a ocorrência do evento $B$ , representada por $P(A | B)$ , é a probabilidade de ocorrer $A$ e $B$ dividida pela probabilidade do evento $B$ .

$P(A | B)=\frac{n(A\cap B)}{n(B)}\,, \, n(B)\neq 0$

OBS 1: Quando as quantidades a serem analisadas para uma probabilidade condicional aparecem numa tabela/quadro, as informações devem ser retiradas numa mesma coluna ou mesma linha. Fique atento!

OBS 2: Na determinação de uma quantidade de números numa lista de números naturais consecutivos aparece como opção a utilização das relações definidas pela Progressão Aritmética (P.A).

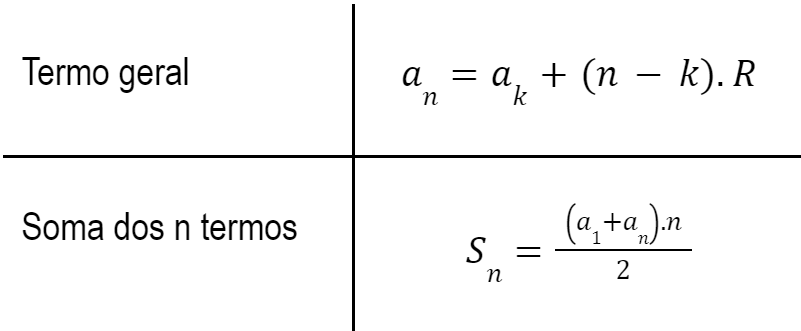
OBS 3: Na Probabilidade Condicional o espaço amostral inicial sempre sofrerá uma redução e, então, o evento será analisado nesse novo espaço amostral.