Relações e funções

Por: Aline Ribeiro 

 

1. Produto cartesiano: Dado dois conjuntos, o produto cartesiano deles será o conjunto de todos os pares ordenados contendo um elemento de cada um dos conjuntos. Matematicamente definimos como:  

A x B = (x, y) | x A  e y B

 

Exemplo: Considere A = 1, 2 , 3 e B = 5, 6, 7, 8, então produto cartesiano de A por B será: 

               A x B =(1,5), (1,6), (1,7), (1,8), (2,5), (2,6), (2,7), (2,8), (3,5), (3,6), (3,7), (3,8) 

 

Graficamente esse produto cartesiano pode ser representado por:

 

 

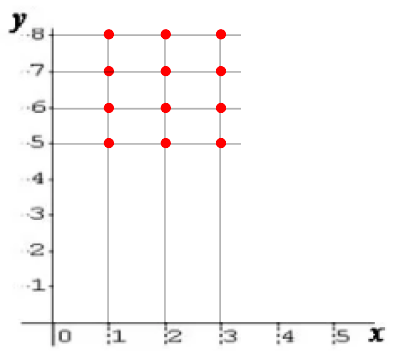
Observação: Para determinar a quantidade de elementos que um produto cartesiano possui, basta fazer o produto entre as quantidades de elementos dos conjuntos. 

2. Relações: Uma relação é uma associação entre dois conjuntos. Nada mais é do que o subconjunto de um produto cartesiano. 

 

Exemplo: Considere A = 1, 2 , 3 e B = 5, 6, 7, 8 e R uma relação do conjunto A com o conjunto B:

 R: AB

R = 1, 5, 2, 5, 3, 7

 

Outra representação possível é através do diagrama de flechas:

 

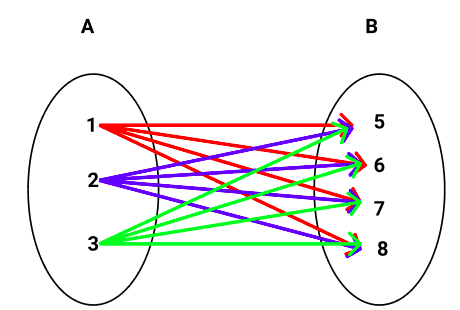
3. Diagrama de flechas: O diagrama de flechas é a representação de dois conjuntos (ilustrado pelas elipses) e suas respectivas ilustrações (ilustrado pelas flechas). 

O conjunto de onde saem as flechas é chamado de conjunto de partida e o conjunto que recebem as flechas é chamado de contradomínio.

 

 

3.1. Domínio: São todo os elementos do conjunto partida que participam da relação (são os elementos de onde saem as flechas).

 

    

 

 

3.2. Imagem: São todos os elementos do contradomínio que participam da relação (são os elementos que recebem flechas).

 

 

       

 

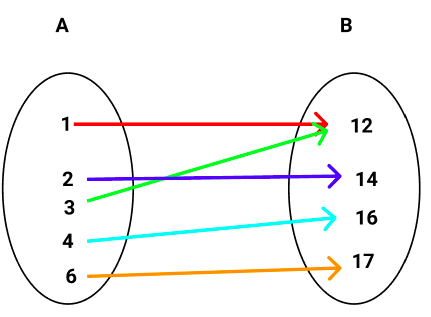
3.3. Exemplo: Considere A = x Z | 1x6_, B = x Z | 12x17 e  R: AB com R=(1, 12),(2, 14),(3, 12),(4, 16),(6, 17). Defina o conjunto de partida, o contradomínio, a imagem e o domínio dessa relação.

 

Como a relação vai de A para B, então o conjunto de partida é o conjunto A e o contradomínio é o conjunto B. 

O domínio e a imagem contém somente os elementos que foram utilizados na relação, desse modo: 

Domínio = 1, 2, 3, 4 , 6

 Imagem = 12, 14, 16, 17

 

4. Funções: É uma relação especial entre dois conjuntos. Que segue uma regra ou lei.

Uma relação só será função se obedecer a lei vigente e se cada elemento do domínio estiver associado a um único elemento do contradomínio. 

 

Exemplos: a) Observe o diagrama: 

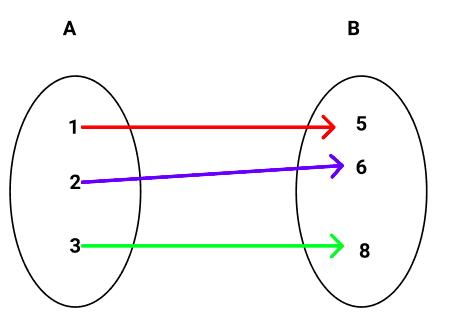
O diagrama de flechas acima representa uma função, pois todos os elemento do domínio estão ligados a um único elemento do contradomínio. 

 

b)  Observe o diagrama: 

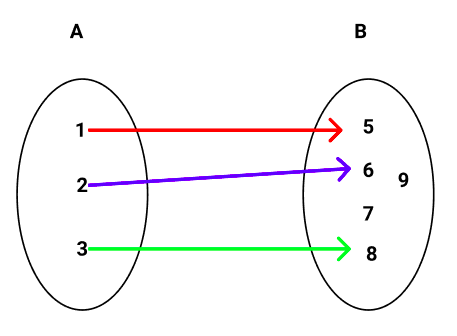
O diagrama de flechas acima representa uma função, pois todos os elemento do domínio estão ligados a um único elemento do contradomínio. 

 

c) Observe o diagrama: 

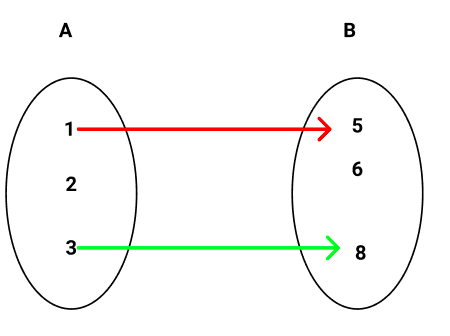
O diagrama de flechas acima não representa uma função, pois existe elementos no domínio que não estão ligados a elementos do contradomínio.

 

d)  Observe o diagrama: 

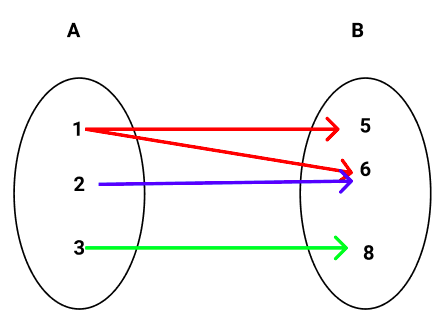
O diagrama de flechas acima não representa uma função, pois um único elemento do domínio possui dois elementos do contradomínio.

 

Observação: Como a função é uma relação, ela também possui domínio e imagem, e podem ser determinados da mesma maneira que em uma relação.