Resumo de matematica: Função Exponencial
Comportamento gráfico e Propriedades
Chama-se de função exponencial qualquer função de
em
dada por uma lei da forma
, em que a é um número real,
. Podemos analisar a função exponencial segundo dois casos:
- 1° caso:
Ex:
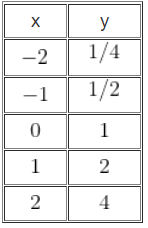
- 2° caso:
Ex:
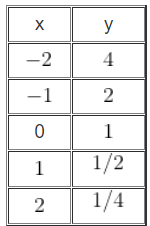
É importante perceber as seguintes características sobre a função exponencial:
I) e
;
II) Para a função é crescente;
III) Para a a função é decrescente;
IV) O gráfico não intercepta o eixo das abscissas. Esse eixo é chamado de assíntota do gráfico da função exponencial.
Equação Exponencial (Redução à mesma base)
As equações que se apresentam com a incógnita no expoente, com bases positivas e diferentes de 1, são chamadas de equações exponenciais.
Exemplos
a)
b)
Em geral, para resolver uma equação exponencial, igualam-se as bases das potências dos dois membros e comparam-se os seus expoentes, ou seja:
Exemplos:
a)
b)
Equação Exponencial (Uso de artifícios)
As equações que se apresentam com a incógnita no expoente, com bases positivas e diferentes de 1, são chamadas de equações exponenciais.
Exemplos
a)
b)
Algumas equações exponenciais, será necessário fazer algumas transformações e usar artifícios. Um desses artifícios é a substituição de uma parte da equação por uma incógnita auxiliar.
Exemplos:a)
Substituindo na equação exponencial, temos:
Voltando a igualdade , obtemos:
b)
Substituindo na equação exponencial, temos:
Voltando a igualdade , obtemos:
Não convém
Inequação Exponencial
Inequação exponencial é uma desigualdade que apresenta a incógnita no expoente de pelo menos uma potência.
Exemplos:
a)
b)
Podemos analisar a função exponencial segundo dois casos:
- 1° caso:
- 2° caso:
Exemplos
a)
b)
Aplicações
DICA 1: Nas equações em que a variável aparece na base da equação, é obrigatório testar os números ,
e
.
Exemplo:
Devemos examinar inicialmente se ,
ou
são soluções da equação.
Substituindo na equação proposta, temos:
(verdadeiro)
Logo, é solução.
Substituindo na equação proposta, temos:
(falso)
Logo, não é solução.
Substituindo na equação, temos:
(verdadeiro)
Logo, é solução da equação.
Supondo agora , temos:
. Os valores
ou
são soluções, pois satisfazem a condição
DICA 2: Nos sistemas de equações exponenciais é necessário a retirada das bases utilizando as propriedades de potências e também a igualdade , com
.
DICA 3: Para as questões de gráficos onde são fornecidos alguns pontos, deve-se substituir os pontos na equação da função dada pela questão para a construção do sistema.
DICA 4: Na resolução das inequações exponenciais, se faz necessário o uso das propriedades:
- 1° caso:
- 2° caso:






