Resumo de matematica: Estudo Geral das Funções III
Paridade das funções
Função Par
Uma função real é dita par se, e somente se, elementos simétricos do domínio gerarem imagens iguais.
Ex: é uma função par, pois:
Representação gráfica
Atenção: O gráfico de uma função par é simétrico em relação ao eixo .
Função Ímpar
Uma função real é dita ímpar se, e somente se, elementos simétricos do domínio gerarem imagens simétricas.
Exemplo: é uma função ímpar, pois:
Representação gráfica
Atenção: O gráfico de uma função ímpar é simétrico em relação origem.
OBSERVAÇÃO
Quando uma função não for par, não quer dizer que será ímpar. Esse tipo de função será classificada como função sem paridade.
Introdução à Função Composta
Considere as funções:
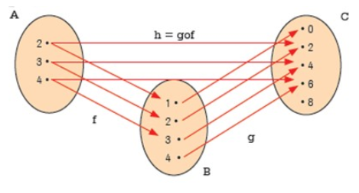
Sejam as funções e
, chama-se composta de
em
, a aplicação de
em
, definida por
.
Observações:
I. A função composta pode ser representada também por:
II. A função composta só estará definida de o contradomínio de for igual ao domínio de
.
Função Composta - Outros exemplos
Função Composta
Sejam as funções e
, chama-se composta de
em
, a aplicação de
em
, definida por
.
Observações
I. A função composta pode ser representada também por:
II. A função composta só estará definida de o contradomínio de for igual ao domínio de
.
Ex 1: Considerando as funções reais e
, determine:
a)
b)
c)
d)
Ex 2: Considerando as funções reais e
, determine
.
Ex 3: Considerando a função real , determine:
a)
Fazendo , temos que
.
Assim,
b)
Fazendo , temos que
Assim,
Sendo , tem-se que
.
Introdução à Função Inversa
Seja uma função bijetora, então a relação
, chama-se função inversa de
.
Notação
Representando por meio de diagramas, temos:
Observações
I. ;
II. ;
III. Se , sendo
invertível, então
e
.
Função Inversa - Outros exemplos
Seja uma função bijetora, então a relação
, chama-se função inversa de
.
Determinação da inversa de uma função
1. Par ordenado
Exemplo
2. Lei de formação
Passo 1) Trocam-se e
de posição;
Passo 2) Isola-se o valor de .
Exemplo
Calcule a inversa da função .
(Trocando
e
de posição);
(Isolando
);
Portanto, a inversa de é a função
.
3. Gráfico
Se , então
. Portanto,
e
terão gráficos simétricos em relação à 1ª bissetriz
;
Aplicações
Função Par
Uma função real é dita par se, e somente se, elementos simétricos do domínio gerarem imagens iguais.
Função Ímpar
Uma função real é dita ímpar se, e somente se, elementos simétricos do domínio gerarem imagens simétricas.
FUNÇÃO COMPOSTA
Sejam as funções e
, chama-se composta de
em
, a aplicação de
em
, definida por
.
Atenção
FUNÇÃO INVERSA
Seja uma função bijetora, então a relação
, chama-se função inversa de
.
OBSERVAÇÕES
I. ;
II. e
;
III. Se , então
. Portanto,
e
terão gráficos simétricos em relação à 1ª bissetriz
;
IV. Cálculo algébrico da função inversa
Passo 1) Trocam-se e
de posição;
Passo 2) Isola-se o valor de .
V. Sendo uma função invertível, podemos afirmar que:
Atenção

Exemplo






