Resumo de matematica: Estudo dos Logaritmos II
MUDANÇA DE BASE
Existem situações em que nos deparamos com um logaritmo em certa base e temos de convertê-lo para outra base.
Um exemplo disso é que, para aplicarmos as propriedades operatórias, os logaritmos devem estar todos na mesma base. Caso contrário, é necessário executar uma mudança de base.
Atenção
Consequências da mudança de base
I)
II)
III)
MUDANÇA DE BASE - Aplicações
| Procedimento | Consequências |
|---|---|
|
|
Exemplos
1) Sendo e
, calcule o valor de
.
2) Calcule o valor de .
FUNÇÃO LOGARÍTMICA
Considerando uma função exponencial do tipo , definida de
em
. Sendo a função
bijetora, tem-se que existe uma função inversa
, definida de
em
, tal que
.
Cálculo da inversa de .
→ Troca-se
por
e
por
→ Isola-se
.
OBSERVAÇÃO
Os gráficos de e
serão simétricos em relação à 1ª bissetriz
.
DEFINIÇÃO
Dado um número real (com
), chama-se função logarítmica de base b a função de
em R dada pela lei
.
1º caso:
Ex:
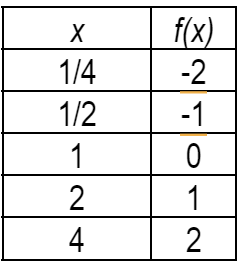
2º caso:
Ex:

É importante perceber as seguintes características sobre a função logarítmica:
I) e
;
II) Para a função é crescente;
III) Para a a função é decrescente;
IV) O gráfico não intercepta o eixo das ordenadas. Esse eixo é chamado de assíntota do gráfico da função logarítmica.
FUNÇÃO LOGARÍTMICA - Outros exemplos
Dado um número real (com
), chama-se função logarítmica de base
a função de
em
dada pela lei
.
1º caso: 2º caso: 0 < b < 1
Ex: Ex:
Atenção
É importante levar em consideração a condição de existência dos logaritmos. Assim, uma função dada por , tem-se que
e
.
Exemplo
Determine o conjunto formado pelos possíveis valores inteiros de de modo que a função
seja crescente.
- Condição de existência
-
-
- Função crescente
Assim, e os números inteiros que validam essa condição são: 4, 5, 6 e 7.
COLOGARITMO
Chamamos de cologaritmo de um número positivo em uma base
e indicamos
o logaritmo do inverso desse número
na base
.
Assim,
Uma consequência imediata é:
Exemplos
a)
b)






