Resumo de matematica: Trigonometria - Álgebra (Trigonometria - Funções)

Função seno.

A função seno é definida por $f(x)=sen(x)$ , com $f:\mathbb{R}\rightarrow \mathbb{R}$ e é uma função circular, pois, basta pensarmos no ciclo trigonométrico, no qual, após a 1ª volta, os valores do seno repetem-se todos na 2ª volta, e na 3ª volta também e em todas as demais. Vale também se percorrermos a circunferência no sentido horário e, neste caso, seriam valores negativos da variável “x”, que representa os valores dos arcos.
Dessa forma, o gráfico que representa a função seno é

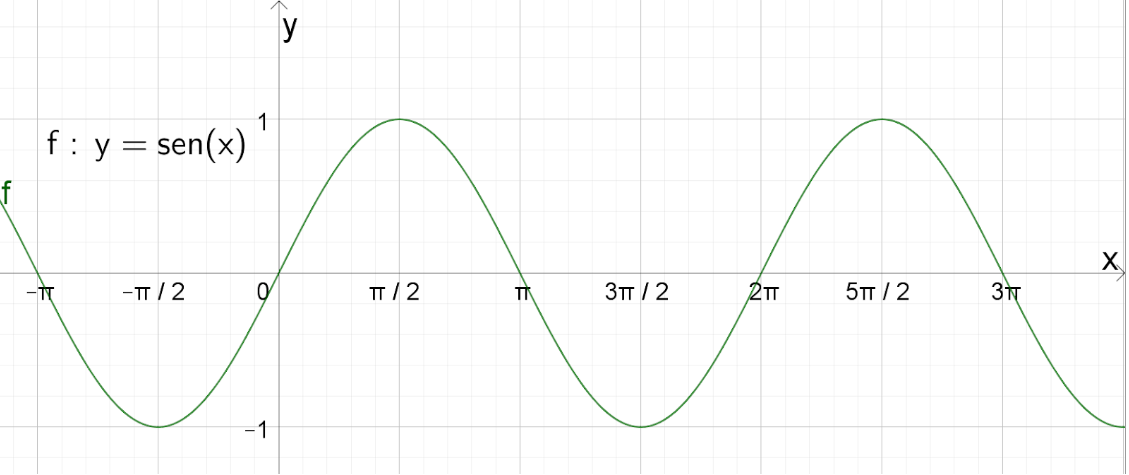
Período da função corresponde a um “comprimento de onda”, como dizemos na Física. No caso da função seno, perceba que uma onda inicia-se em $x=0$ e termina em $x=2\pi$ , onde começa novamente uma outra onda idêntica. Nesse caso o período é $2\pi$ .

Função Seno - Gráfico

A imagem da função seno $f(x)=sen(x)$ , definida em $\mathbb{R}$ , é $\left [ -1,1 \right ]$ . Mas quando inserimos outros elementos à lei de associação desta função, usando a composição de funções, a imagem pode mudar. Com isso, no caso da função $g(x)=a+b\cdot sen(cx+d)$ , a e b, provocam alterações verticais no gráfico da função seno, sendo que o a provoca deslocamento enquanto b estica ou encolhe o gráfico. Assim, a imagem dessa função $g(x)$ fica $\left [ a-\left | b \right |,a+\left | b \right | \right ]$ .

Da mesma forma que a imagem pode se alterar, o período também. As constantes reais c e d provocam alterações horizontais. No caso, c estica ou encolhe, enquanto d desloca. Sendo assim, enquanto que o período de $f(x)$ é $2\pi$ , o período de $g(x)$ é $\frac{2\pi }{\left | c \right |}$ .

Função cosseno.

A ideia de deformações e deslocamentos do gráfico da função seno vale também para a função cosseno. Com isso, seja a função $f(x)=a+b\cdot cos(cx+d)$ , definida em $\mathbb{R}$ , a e b provocam alterações verticais enquanto que c e d provocam alterações horizontais e, ainda, os resultados do conjunto imagem e período são os mesmos para seno e cosseno.

Sendo assim, se quisermos encontrar os valores de máximo e mínimo de uma função seno ou cosseno, definidas em $\mathbb{R}$ , basta lembrarmos que $-1\leq sen(x)\leq 1$ e $-1\leq cos(x)\leq 1$ . Por exemplo, na função $g(x)=3-2\cdot cos(2x-2)$ , definida em $\mathbb{R}$ , tem seu máximo e mínimo determinados quando cosseno é -1 e 1, respectivamente, ou seja, seu máximo é $3-2(-1)=5$ e seu mínimo é $3-2\cdot1=1$ .

Função cosseno.

Para determinarmos a lei de associação de uma função trigonométrica a partir do seu gráfico, devemos analisar as modificações e confrontá-las com os parâmetros. Por exemplo, para que valores de “a”, “b”, “c” e “d”, o gráfico da função, cuja lei é $f(x)=a+b\cdot cos(cx+d)$ , é o da figura abaixo?

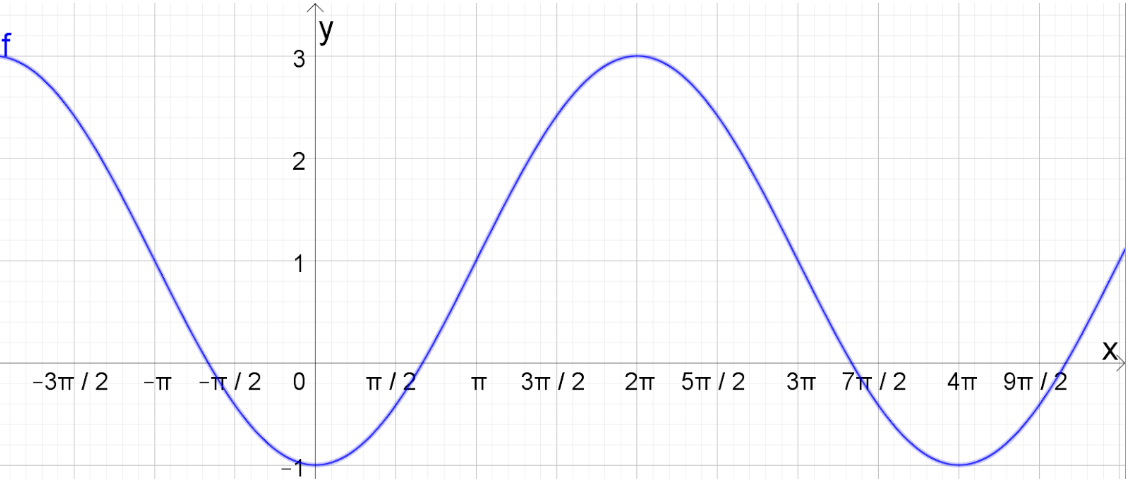
Como a amplitude é $3-(-1)=4$ , então o módulo do valor de “b” é 2. Se a fosse igual a 1, então a variação da função seria de -2 a 2, mas como é de -1 a 3, ou seja, “subiu” uma unidade, então a = 1. A função deveria interceptar o eixo y inicialmente em 3, mas como inicia “embaixo”, significa que ela foi invertida, ou seja, “b” é negativo, portanto, $b=2$ . Por fim, como o período é 4, então $c=2$ . Como não houve deslocamento horizontal, $d=0$ .

Função tangente.

No gráfico da função tangente existem linhas que limitam o gráfico chamadas de assíntotas, ou seja, o gráfico aproxima-se infinitamente essa linha, mas nunca a toca. Isso acontece porque existem valores de arcos para os quais a função não existe, como 90° $(\frac{\pi}{2} \,rad)$ . Quando pensamos no ciclo trigonométrico, toda vez que o arco “passa” pelo 90° ou outro congruente ao 90° ou ainda pelo 270° e seus côngruos, a tangente não existe.

Com isso, o gráfico da função tangente em R fica com várias retas assíntotas. Vejamos a figura abaixo.

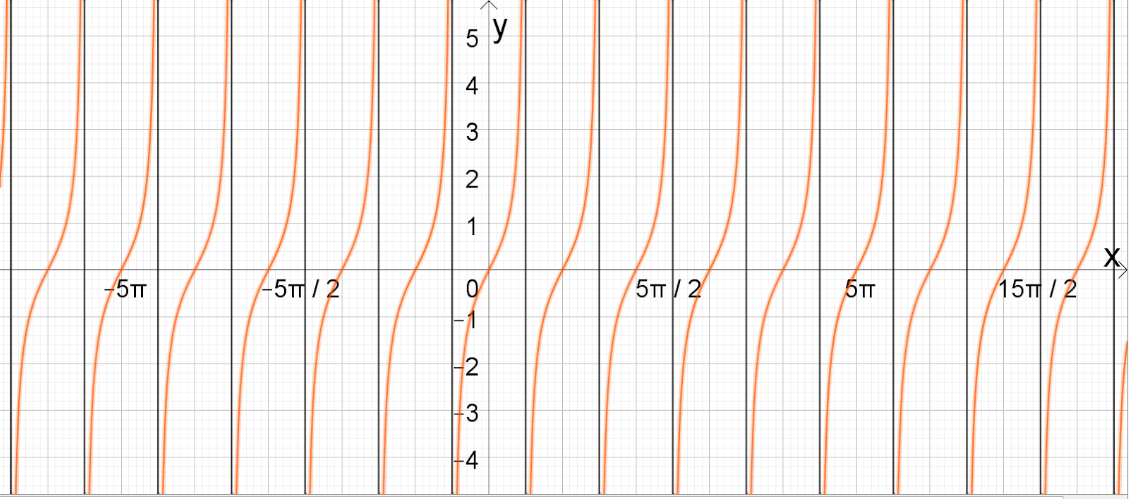
Função tangente. (Exercícios Resolvidos)

Análise de gráficos é uma situação recorrente em provas de vestibular. Quando o gráfico corresponde a uma função trigonométrica, precisamos saber quais são os parâmetros “inseridos” na função seno, cosseno ou tangente. Por exemplo, vamos analisar o problema abaixo.

(ENEM - 2021)

Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo $\displaystyle P (t)= \pm A\, cos\left ( \omega t \right)$ ou $\displaystyle P (t)= \pm A\, sen\left ( \omega t \right)$ , em que A > 0 é a amplitude do deslocamento máximo e $\omega$ é a frequência, que se relaciona com o período T pela fórmula $\omega = \frac{2\pi }{T}$ .

Considera a ausência de quaisquer forças dissipativas.

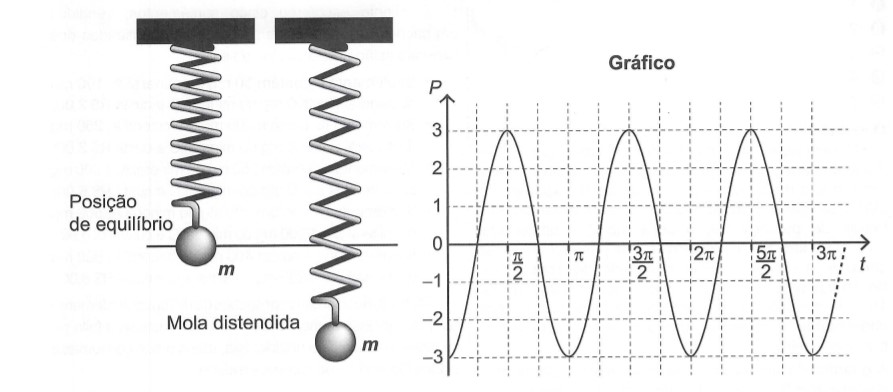
A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo no gráfico, é

a) $-3cos(2t)$

b) $-3sen(2t)$

c) $3cos(2t)$

d) $-6cos(2t)$

e) $6cos(2t)$

Solução:
Como nas leis sugeridas no problema não existe parâmetro sendo somado ou subtraído a x, então o gráfico não sofre deslocamento horizontal e como seu início (origem) não é no ponto (0, 0), então não será o gráfico de uma função seno, mas sim do cosseno. Se seu início na origem é negativo, então A tem valor negativo. Se a imagem é $Im=\left [ -3,3 \right ]$ , então $A=-3$ . Como o período é $\pi$ , então $w=2$ . Portanto, resposta correta é letra “b”.