SISTEMA DE NUMERAÇÃO DECIMAL

O sistema de numeração decimal é usado corriqueiramente para indicar quantidades. O nome decimal vem do fato de que o sistema é dotado de dez algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Cada algarismo sozinho representa uma quantidade de zero a nove, e os números maiores do que nove, são representados por dois ou mais desses algarismos, de modo que os valores representados por cada algarismo dependem da posição que esses algarismos ocupam nas cifras numéricas.
Veja que, por exemplo, o número duzentos e vinte e dois é escrito com três algarismos iguais, mas cada algarismo 2 representa uma quantidade diferente desse número.
Da esquerda para a direita, na cifra 222, o primeiro algarismo 2 representa duzentas unidades, o segundo algarismo 2, no centro da cifra, representa vinte unidades, e o terceiro e último algarismo 2 representa apenas duas unidades.
Há uma conexão entre a posição ocupada pelo algarismo e a quantidade de unidades que ele representa.
Essa conexão combina os aspectos ordinal e cardinal dos números naturais, e relaciona esses valores por meio das operações de adição, multiplicação e potenciação.
Toda cifra numérica decimal com dois ou mais algarismos representa uma sentença aritmética formada pelas operações de adição, multiplicação e potenciação, na qual os símbolos (+) e ( ⋅ ) bem como os expoentes das potências são todos omitidos. As normas da leitura do número cifrado já consideram essas operações.
Nessas representações decimais, todo algarismo que não ocupa a posição final de uma cifra numérica deve ser lido como um múltiplo de uma potência de base 10. Veja a nomenclatura das posições dos algarismos de uma cifra numérica decimal:

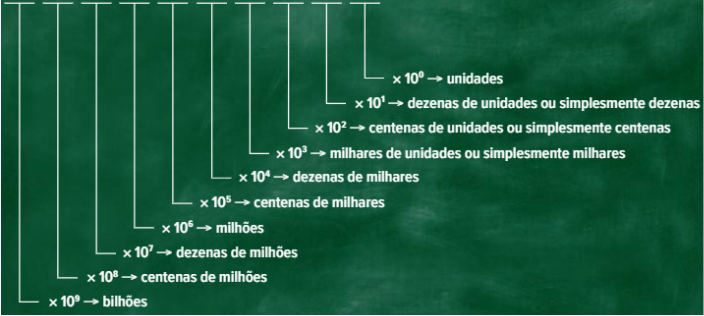
O sistema decimal tem a base b = 10, que pode ser omitida no final da cifra:

(3 458)₁₀ = 3 458 = 3 ⋅ 10³ + 4 ⋅ 10² + 5 ⋅ 10¹ + 8 · 10⁰ = 3 000 + 400 + 50 + 8

Assim, quando um número como, por exemplo, 3 458 é lido em voz alta, ouve-se “três mil e quatrocentos e cinquenta e
oito”, o que indica a adição dos números: 3 000, 400, 50 e 8, pois a conjunção “e” é aditiva.
No sistema decimal, pode-se usar um recurso mnemônico para cifrar números de até quatro algarismos, que é bastante útil.
As letras u, d, c e m, iniciais das palavras unidade, dezena, centena e milhar são colocadas nos lugares dos respectivos
algarismos desconhecidos na cifra de um número.

Exemplos:
(du) = 10 ⋅ d + u
(cdu) = 100 ⋅ c + 10 ⋅ d + u
(mcdu) = 1000 ⋅ m + 100 ⋅ c + 10 ⋅ d + u

 

SISTEMAS MÉTRICOS

Grandezas físicas são aquelas grandezas que podem ser medidas, ou seja, que descrevem qualitativamente e quantitativamente as relações entre as propriedades observadas no estudo dos fenômenos físicos.

Exemplos
a) comprimento 
b) massa 
c) volume 
d) tempo

As Unidades de Medida são representações das grandezas físicas utilizadas em diversas áreas do conhecimento com o intuito de quantificar uma matéria, uma sensação, o tempo ou o tamanho de algo, por exemplo.
 
A necessidade de fazer medições sempre fez parte da história da humanidade e da origem das civilizações. Contudo, como cada região possuía seu próprio sistema arbitrário de medidas, que geralmente se baseava em partes do corpo humano, como palmo, polegada, pé e jarda, as medições eram imprecisas e variavam muito. 
Durante décadas, os comerciantes foram os mais prejudicados com a falta de padrão das medidas, afinal, os diversos sistemas diferentes causavam problemas na hora de comparar tamanhos, pesos e comprimentos.
A criação do sistema métrico decimal foi uma proposta da França, por volta de 1790, em plena época de Revolução Francesa (1789-1799).  A ideia surgiu como tentativa do governo francês de unificar as medidas, para acabar com as dificuldades do comércio e da indústria.
Para acabar de vez com os sistemas arbitrários e pouco confiáveis de medição, foi criado o sistema métrico decimal.
 
Em todo o mundo as unidades de medida seguem um padrão determinado pelo Sistema Internacional de Unidades (SI). A partir da unidade-padrão estabelecida pelo Sistema Internacional, podemos ainda utilizar outras unidades derivadas dela, o que permite compararmos e ampliarmos a noção quantitativa da grandeza.
 

Unidades de medida de comprimento

A unidade padrão de medida de comprimento é o metro.

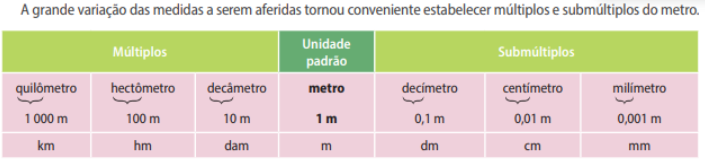
Outras unidades de medidas de comprimentos
Existem outras unidades de medidas de comprimento bastante comuns, sendo elas:
 
• Polegada: utilizada para medir-se tela de smartphone, notebook e demais aparelhos eletrônicos. É denotada geralmente pelo número seguido de duas aspas, por exemplo 40” (lê-se: 40 polegadas). Uma polegada corresponde a 2,54 cm.
 
• Palmo: utilizado para medir-se objetos um pouco maiores do que os que medimos com polegadas, e é pouco usado atualmente. 
Um palmo corresponde a 22,86 cm.
 
• Pé: utilizado até hoje para situar-se quanto à altura de um avião. Para representar uma distância medida em pés, colocamos o número seguido de uma aspa, por exemplo 30’(lê-se: 30 pés). 
Um pé corresponde a 30,48 cm.
 
• Jarda: utilizada nos EUA, sendo comum no futebol americano. Uma jarda corresponde a 0,9144 m.
 
• Légua: utilizada antigamente para medir-se distâncias maiores, a légua era bastante comum na navegação. Uma légua corresponde a 4,82803 quilômetros.
 
• Milha: utilizada para medir-se distâncias maiores, tendo sido bastante comum nos povos antigos. Uma milha corresponde a 1,60934 km.
 
• Ano-luz: utilizado para medir-se a distância entre astros, sendo muitas vezes confundido com medida de tempo. 
Um ano-luz corresponde a 9 460 730 472 580,8 km.

 

Unidades de medida de área

A unidade padrão de medida de área é o metro quadrado.

Unidades agrárias

As unidades agrárias são unidades de medida de superfície usadas, principalmente, em áreas rurais. Dentre essas unidades, destacamos o alqueire, o are e o hectare. 

Alqueire 

Essa unidade de media é bastante utilizada, mas varia de acordo com a região do País. Temos, por exemplo, que: 

• 1 alqueire paulista equivale a 24 200 m² ; 
• 1 alqueire do Norte equivale a 27 225 m2 ; 
• 1 alqueire mineiro equivale a 48 400 m² ; 
• 1 alqueire baiano equivale a 96 800 m² . 

Devido às variações, quando for necessário converter unidades que envolvam o alqueire, deve-se informar a correspondente equivalência em metros quadrados (ou em outra unidade de medida de área) a ser utilizada. 
No Sul do Brasil é usado o alqueire com 24200 m² . 

Are 
Um are (1 a) corresponde a cem metros quadrados. 

1 a = 100 m²

Hectare 
Um hectare (1 ha) corresponde a cem ares (100 a), ou seja, equivale a uma área de dez mil metros quadrados. Essa é a unidade agrária mais utilizada atualmente. 

1 ha = 100 a = 100 . (100 m² ) = 10 000 m² 
1 ha = 10 000 m²

Observe ainda que um hectare corresponde a um hectômetro quadrado (100 m . 100 m).

 

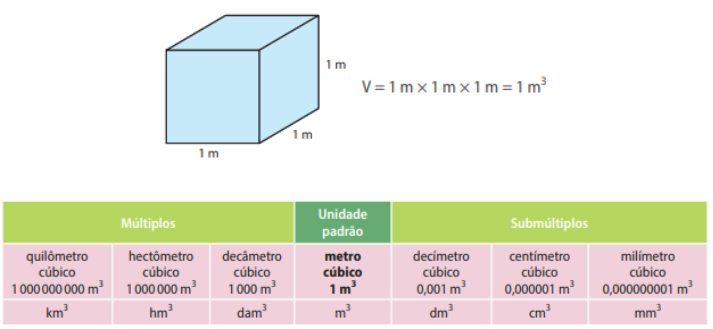
Unidades de medida de volume

A unidade padrão de medida de volume é o metro cúbico.
O volume de um corpo é a quantidade de espaço ocupado por esse corpo.

Unidades de medida de capacidade

Considere capacidade como sendo o volume máximo que pode ser armazenado no interior de um recipiente. 
A principal unidade de medida de capacidade é o litro.

Um litro é o volume equivalente a um decímetro cúbico. Portanto, nas aplicações práticas, considera-se que 1 litro = 1 dm³. 
Nas conversões de unidades, as equivalências mais usadas são: 

• 1 mL = 1 cm³ 
• 1 litro = 1 dm³ 
• 1000 litros = 1 m³ 
• 1 litro = 1000 mL
 

SISTEMA DECIMAL E SISTEMAS MÉTRICOS 

DICA 1 

Um número natural N = α_n α_{n – 1} α_{n – 2} α_{n – 3} ... α₂ α₁ α₀ , com α_n,α_{n – 1}, α_{n – 2}, α_{n – 3}, ..., α₂, α₁, α₀  {0; 1; 2; ...; 9} no sistema decimal pode ser escrito na forma:

N = α_n . 10ⁿ + α^{_{n – 1}} . 10^{n – 1} + α_{n – 2} . 10^{n – 2} + α_{n – 3} . 10^{n – 3} + ... + α₂ . 10² + α₁ . 10¹ + α₀ . 10⁰

Assim, por exemplo, um número com dois algarismos pode ser escrito na forma ab = a . 10¹ + b . 10⁰, com a, b  {0; 1; 2; ...; 9} e a ≠ 0.

DICA 2 

Numa igualdade com duas variáveis, sugere-se a construção de uma tabela de valores levando em consideração as possibilidades dentro das restrições pré-estabelecidas. 

DICA 3
 
A direção das transformações numa questão objetiva deverá ser guiada pela unidade das alternativas.

DICA 4

Nas conversões de unidades, as equivalências mais usadas são: 

• 1 mL = 1 cm³ 
• 1 litro = 1 dm³ 
• 1000 litros = 1 m³ 
• 1 litro = 1000 mL
• 1 tonelada = 1000 kg