Resumo de matematica: Trigonometria - Trigonometria no Triângulo Retângulo. (Trigonometria no Triângulo)

Seno, cosseno e tangente de um ângulo

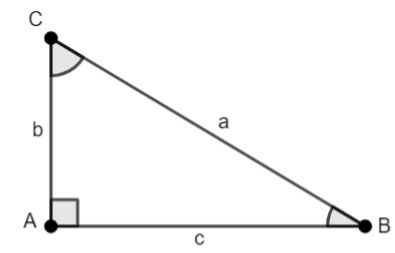
Em um triângulo retângulo, definimos seno, cosseno e tangente como razões entre medidas de dois lados relativos a um determinado ângulo. Seno é a razão entre as medidas do cateto oposto e da hipotenusa, o cosseno é a razão entre as medidas do cateto adjacente e da hipotenusa e a tangente é a razão entre as medidas do cateto oposto e do cateto adjacente.

No triângulo abaixo, temos:

$Sen\,\widehat{C}=\frac{c}{a}$

$Cos\,\widehat{C}=\frac{b}{a}$

$tg\,\widehat{C}=\frac{c}{b}$

$Sen\,\widehat{B}=\frac{b}{a}$

$Cos\,\widehat{B}=\frac{c}{a}$

$tg\,\widehat{B}=\frac{b}{c}$

Secante, cossecante e cotangente de um ângulo. (Tabela Trigonométrica e Ângulos Notáveis)

Razão trigonométrica estabelece a relação entre dois lados de um triângulo retângulo e um dos seus ângulos que não seja o ângulo reto. E para isto, deve-se conhecer o valor do seno, cosseno ou tangente do ângulo em questão. Existe uma tabela, chamada de tabela trigonométrica, que informa os valores de seno, cosseno e tangente para todos os valores inteiros de ângulos de 1° a 89°.
Esta tabela ou seus valores são fornecidos nas provas a não ser que estes ângulos sejam 30°, 45° e 60°, que chamamos de ângulos notáveis, e seus valores são:

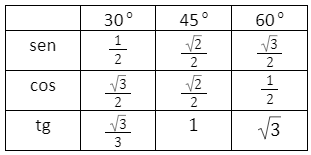
Ângulos Notáveis. (Lei dos Senos e Lei dos Cossenos)

Além das razões trigonométricas mais comuns em um triângulo retângulo que são seno, cosseno e tangente, também existe o inverso de cada uma dessas razões, chamadas de secante, cossecante e cotangente, que são as razões inversas do cosseno, seno e tangente, respectivamente.
Assim, no triângulo retângulo abaixo, essas razões são:

$Sec\,\widehat{C}=\frac{a}{b}$

$Cossec\,\widehat{C}=\frac{a}{c}$

$Cotg\,\widehat{C}=\frac{b}{c}$

$Sec\,\widehat{B}=\frac{a}{c}$

$Cossec\,\widehat{C}=\frac{a}{b}$

$Cotg\,\widehat{C}=\frac{c}{b}$

Exemplos. (Exercícios Resolvidos)

Para triângulos retângulos, quando necessário, utilizam-se as razões trigonométricas de seno, cosseno e tangente. Mas se os triângulos não são retângulos, essas razões não podem ser utilizadas diretamente. Como isso, faz-se necessário a utilização da Lei dos Senos e da Lei dos Cossenos.
A Lei dos Senos é

$\frac{a}{sen\,\widehat{A}}=\frac{b}{sen\,\widehat{B}}=\frac{c}{sen\,\widehat{C}}=2R$ ,

sendo a, b, c as medidas dos lados de um triângulo e seus respectivos ângulos opostos medem $\widehat{A}$ , $\widehat{B}$ , $\widehat{C}$ , além de $2R$ ser a medida do diâmetro da circunferência circunscrita a este triângulo.
A Lei dos Cossenos é

$a^2=b^2+c^2-2bc\cdot Cos\widehat{A}$

sendo a, b, c as medidas dos lados de um triângulo cujo ângulo oposto ao lado de medida a é $\widehat{A}$ .

Muitos problemas de trigonometria fornecem uma das relações trigonométricas em um triângulo retângulo e querem saber o valor de outra relação trigonométrica. Um caminho para resolver este tipo problema é usar a Relação Fundamental da Trigonometria

$Sen^2(\alpha )+Cos^2(\alpha )=1$

e a relação entre as três principais relações trigonométricas:

$tg(\alpha )=\frac{sen(\alpha )}{cos(\alpha )}$

Mas uma maneira mais rápida para solucionar estes problemas é usar o Teorema de Pitágoras em um triângulo retângulo auxiliar, por exemplo, se o seno de um ângulo de um triângulo retângulo é $\frac{1}{3}$ , construímos um triângulo retângulo e chamamos utilizamos 1 (numerador da fração) como medida do seu cateto oposto do referido ângulo e 3 (denominador) como medida de sua hipotenusa. Aplicando o Teorema de Pitágoras, encontramos $2\sqrt{2}$ para a medida do cateto adjacente. Agora, é possível calcular qualquer razão trigonométrica relativo ao ângulo em questão, usando este triângulo.