Um cilindro metlico, com 1 m de dimetro e 2,5 m de
Um cilindro metálico, com 1 m de diâmetro e 2,5 m de altura, serve como tanque para armazenar um combustível com densidade de 800 kg/m3 . Quando o tanque está fechado e abastecido com uma coluna de combustível de 2 m de altura, a pressão na superfície do combustível armazenado no cilindro é de 4,48×105 Pa. Com base nessas informações, responda aos itens a seguir.
a) Acidentalmente, é feito um furo circular neste tanque a 0,5 m acima de sua base, cujo diâmetro é de 1 mm, como representado na figura a seguir (note que a figura não está em escala)
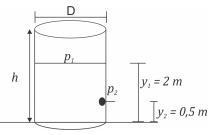
Esse furo só foi observado 1 hora após o ocorrido. Calcule a quantidade de litros de combustível que vazou pelo furo nesse intervalo de tempo. Utilize g = 10 m/s2 e π = 3. Sabe-se que 1 mm = 10−3 m, 1 L = 10−3 m3 e 1 h = 3600 s. Considere a pressão atmosférica = 1×105 Pa. Observação: considere que a velocidade de escoamento do líquido pelo furo (v2) é muito maior que a velocidade com que o nível de combustível decresce (v1). Logo, v1 pode ser desprezada.
b) Consertado o furo, o tanque foi completamente abastecido logo ao raiar do dia. Considerando que os coeficientes de dilatação volumétrica do combustível e do metal do cilindro valem, respectivamente, 10−3 °C−1 e 7×10−5 °C−1 , calcule a quantidade de litros de combustível que transbordaria do tanque se ele permanecesse aberto ao longo do dia, supondo uma variação máxima de temperatura de 20 ◦C. Observação: considere que os volumes iniciais de combustível e do cilindro são iguais (com as dimensões iniciais dadas no enunciado). Despreze as perdas por evaporação do combustível.


