(AFA - 2008)Um projtil de massa m e velocidade v a
(AFA - 2008)
Um projétil de massa m e velocidade v atinge horizontalmente um bloco de massa M que se encontra acoplado a uma mola de constante elástica K, como mostra a figura abaixo.
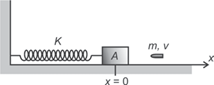
Apos o impacto, o projétil se aloja no bloco e o sistema massa-mola-projétil passa a oscilar em MHS com amplitude a. Não há atrito entre o bloco e o plano horizontal nem resistência do ar. Nessas condições, a posição em função do tempo para o oscilador harmônico simples é dada pela expressão x = a cos(ωt + φ0), onde a e \(\omega\) valem, respectivamente,
\(\sqrt{\frac{(M+m)v}{K}}\) e \(\sqrt{\frac{K}{M+m}}\)
\(\frac{mv}{M+m}\sqrt{\frac{M+m}{K}}\) e \(\sqrt{\frac{K}{M+m}}\)
\(\sqrt{\frac{K}{M+m}}\) e \(\sqrt{\frac{M+m}{K}}\)
\(\frac{M+m}{mv}\sqrt{\frac{K}{M+m}}\) e \(\sqrt{\frac{M+m}{K}}\)


