(AFA - 2021)Considere uma barra homognea, retiline

(AFA - 2021)

Considere uma barra homogênea, retilinea e horizontal fixa em uma de suas extremidades pelo ponto O, e submetida à ação de uma força \(\vec{F}\) na outra extremidade, no ponto P, conforme mostra a Figura 1.

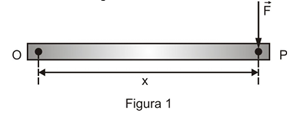
A distância entre os pontos O e P vale x, e a ação da força \(\vec{F}\) gera um torque M₁ na barra, em relação ao ponto de fixação.

Dobrando-se a barra, de acordo com a Figura 2, e aplicando-se novamente a mesma força \(\vec{F}\) no ponto P, um novo torque M₂ é gerado em relação ao ponto O.

Considere que a barra não possa ser deformada por ação da força \(\vec{F}\).

Nestas condições, a razão \(\frac{M_{1}}{M_{2}}\) entre os torques gerados pela força \(\vec{F}\), nas duas configurações apresentadas, é