O nmero N de tomos de um istopo radioativo existen

O número N de átomos de um isótopo radioativo existente em uma amostra diminui com o tempo t, de acordo com a expressão \(N(t)=N_0e^{-\lambda t}\), sendo \(N_0\) o número de átomos deste isótopo em t = 0 e λ a constante de decaimento. Abaixo, está apresentado o gráfico do log10 N em função de t, obtido em um estudo experimental do radiofármaco Tecnécio 99 metaestável (\(^{99m}\textrm{Tc}\)), muito utilizado em diagnósticos do coração.

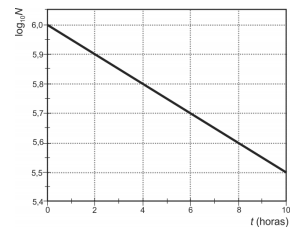
A partir do gráfico, determine

a) o valor de \(log_{10}N_0\) ;

b) o número \(N_0\) de átomos radioativos de \(^{99m}\textrm{Tc}\) ;

c) a meia-vida (\(t_{1/2}\)) do \(^{99m}\textrm{Tc}\).

Note e adote:

A meia-vida (\(t_{1/2}\)) de um isótopo radioativo é o intervalo de tempo em que o número de átomos desse isótopo existente em uma amostra cai para a metade.

\(log_{10}2 = 0,3; log_{10}5 = 0,7\)