[IME- 2015/2016 - 2 fase]Seis blocos idnticos, ide

[IME- 2015/2016  - 2ª fase]

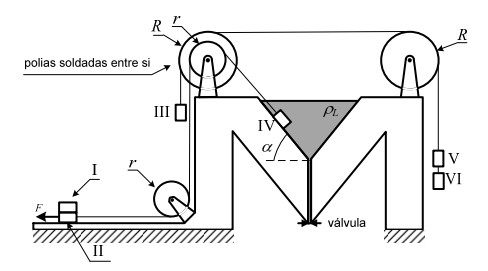
Seis blocos idênticos, identificados conforme a figura, encontram-se interligados por um sistema de cordas e polias ideais, inicialmente em equilíbrio estático sob ação de uma força F, paralela ao plano de deslizamento do bloco II e sentido representado na figura. Considere que: o conjunto de polias de raios r e R são solidárias entre si; não existe deslizamento entre os cabos e as polias; e existe atrito entre os blocos I e II e entre os blocos II e IV com as suas respectivas superfícies de contato. Determine:

a) o menor valor do módulo da força F para que o sistema permaneça em equilíbrio estático;

b) o maior valor do módulo da força F para que o sistema permaneça em equilíbrio estático quando a válvula for aberta e o líquido totalmente escoado;

c) o maior valor do módulo da força F para que não haja deslizamento entre os blocos I e II, admitindo que a válvula tenha sido aberta, o tanque esvaziado e a força F aumentado de modo que o sistema tenha entrado em movimento.

Dados:

• aceleração da gravidade: g;

• massa específica de cada bloco: \(p_{B}\);

• volume de cada bloco: \(V_{B}\);

• massa específica do líquido: \(p_{L}\);

• coeficiente de atrito entre os blocos I e II: μ;

• coeficiente de atrito estático entre o bloco II e o solo: 1,5 μ;

• coeficiente de atrito dinâmico entre o bloco II e o solo: 1,4 μ;

• coeficiente de atrito estático entre o bloco IV e a superfície com líquido: 0,5 μ;

• coeficiente de atrito estático entre o bloco IV e a superfície sem líquido: 0,85 μ;

• coeficiente de atrito dinâmico entre o bloco IV e a superfície sem liquido: 0,75 μ;

• ângulo entre a superfície de contato do bloco IV e a horizontal: α.