(ITA - 2009- 2 fase)Lua e Sol so os principais res

(ITA - 2009 - 2ª fase)

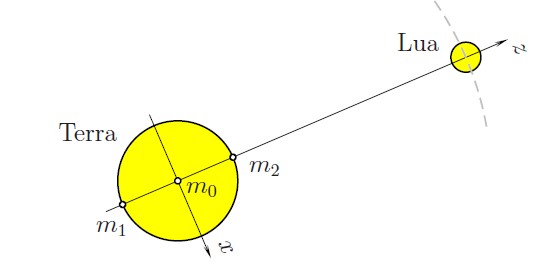
Lua e Sol são os principais responsáveis pelas forcas de maré. Estas são produzidas devido às diferenças na aceleração gravitacional sofrida por massas distribuídas na Terra em razão das respectivas diferenças de suas distâncias em relação a esses astros. A figura mostra duas massas iguais, m1 = m2 = m, dispostas sobre a superfície da Terra em posições diametralmente opostas e alinhadas em relação à Lua, bem como uma massa m0 = m  situada no centro da Terra. Considere G a constante de gravitação universal, M a massa da Lua, r o raio da Terra e R a distância entre os centros da Terra e da Lua. Considere, também, \(f_{0_{z}},f_{1_{z}} \ e \ f_{2_{z}}\)  as forças produzidas pela Lua respectivamente sobre as massas m0, m1 e m2. Determine as diferenças  \((f_{1_{z}}-f_{0_{z}}) \ e \ (f_{2_{z}}-f_{0_{z}})\)  sabendo que devera usar a aproximação   \(\frac{1}{(1+x)^{\alpha}}=1-\alpha x\)  ,  quando x << 1.