(UFPR - 2019 - 1 FASE)Um objeto de massa m constan

(UFPR - 2019 - 1ª FASE)

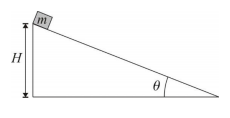
Um objeto de massa m constante está situado no topo de um plano inclinado sem atrito, de ângulo de inclinação \(\theta\), conforme mostra a figura ao lado. O objeto está inicialmente em repouso, a uma altura H da base do plano inclinado, e pode ser considerado uma partícula, tendo em conta as dimensões envolvidas. Num dado instante, ele é solto e desce o plano inclinado, chegando à sua base num instante posterior. Durante o movimento, o objeto não fica sujeito a nenhum tipo de atrito e as observações são feitas por um referencial inercial. No local, a aceleração gravitacional vale, em módulo, g. Levando em consideração os dados apresentados, assinale a alternativa que corresponde ao valor do módulo da quantidade de movimento (momento linear) Q que o objeto de massa m adquire ao chegar à base do plano inclinado.