(UFPR - 2022- 2 fase)Um feixe de luz incide num pr

(UFPR - 2022- 2ª fase)

 

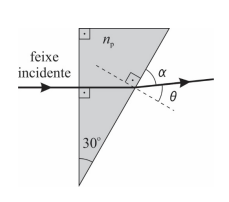
Um feixe de luz incide num prisma triangular. Um dos ângulos internos do prisma é reto, e os outros valem 30° e 60°. Esse prisma está imerso em ar, que tem um índice de refração \(n_{ar}=1\). O feixe incide perpendicularmente em uma das superfícies do prisma vindo do ar, atravessa o prisma e incide noutra superfície do prisma, retornando novamente para o ar, conforme ilustra a figura. O índice de refração do prisma vale \(n_{p}\).

Sabendo que \(sen \ 30 ^{\circ} = cos \ 60 ^{\circ} = \frac{1}{2}, sen \ 60 ^{\circ} = cos \ 30 ^{\circ} = \frac{\sqrt{3}}{2}, sen \ \theta = cos \ \alpha = \frac{3}{5}\) e \(sen \ \alpha = cos \ \theta = \frac{4}{5}\), determine o valor numérico do índice de refração do prisma.