(Unesp 2006) A figura representa, no plano complex
Matemática | números complexos | números complexos na forma algébrica | adição de números complexos na forma algébrica
Matemática | números complexos | números complexos na forma algébrica | conjugado de um número complexo na forma algébrica
Matemática | números complexos | números complexos na forma algébrica | definição de número complexo
Matemática | números complexos | números complexos na forma algébrica | divisão de um número complexo na forma algébrica
Matemática | números complexos | números complexos na forma algébrica | igualdade de números complexos na forma algébrica
Matemática | números complexos | números complexos na forma algébrica | imersão de números reais em números complexos
Matemática | números complexos | números complexos na forma algébrica | multiplicação de números complexos na forma algébrica
Matemática | números complexos | números complexos na forma algébrica | propriedades de um conjugado
Matemática | números complexos | números complexos na forma algébrica | representação algébrica de um número complexo
(Unesp 2006) A figura representa, no plano complexo, um semicírculo de centro na origem e raio 1.
Indique por Re(z), Im(z) e a parte real, a parte imaginária e o módulo de um número complexo z = x + yi, respectivamente, onde i indica a unidade imaginária. A única alternativa que contém as condições que descrevem totalmente o subconjunto do plano que representa a região sombreada, incluindo sua fronteira, é
A
Re(z) ≥ 0, Im(z) ≥ 0 e 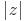 ≤ 1.
≤ 1.
B
Re(z) ≥ 0, Im(z) ≤ 0 e 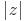 ≤ 1.
≤ 1.
C
Re(z) ≥ 0, e 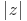 ≥ 1.
≥ 1.
D
Im(z) ≥ 0 e 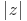 ≥ 1.
≥ 1.
E
Re(z) ≥ 0 e 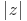 ≤ 1.
≤ 1.


