(UNESP - 2020 - 2 FASE)A modelagem dos sistemas de

(UNESP - 2020 - 2ª FASE) A modelagem dos sistemas de cor é essencial na computação gráfica, e um dos maiores desafios dessa área é a conversão de coordenadas de diferentes sistemas. O sistema RGB pressupõe que o sistema de processamento de cor do olho humano seja baseado nas faixas vermelha (red), verde (green) e azul (blue) do espectro visível. Já o modelo CMY usa cores complementares, ciano (cyan), magenta (magenta) e amarelo (yellow), e foi importante no desenvolvimento de impressoras. As cores no sistema CMY ficam delimitadas por um cubo, o cubo CMY, conforme ilustrado.

 

 

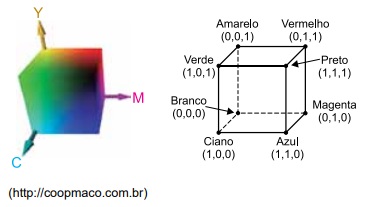
a) A transformação de uma cor no sistema RGB, descrita por (r, g, b), para o sistema CMY, descrita por (c, m, y), é dada por \(\begin{bmatrix}c \\ m \\ y \end{bmatrix} = \begin{bmatrix}1 \\ 1 \\ 1 \end{bmatrix} -\begin{bmatrix}r \\ g \\ b \end{bmatrix}\) . Supondo que uma cor no sistema RGB seja descrita por \(({\frac{1}{4},\frac{1}{100};0})\), apresente as coordenadas dessa cor no sistema CMY e indique qual das oito cores detalhadas no cubo CMY está mais próxima dela.

b) O sistema NTSC (National Television Standards Committee), utilizado em emissões para a televisão, baseia-se na separação dos sinais de cor RGB em um sinal de luminosidade e dois sinais de cromaticidade. Assim como no espaço RGB, as cores no espaço YIQ, utilizado no sistema NTSC, são descritas por coordenadas, sendo representadas por (y, i, q). A relação entre as cores desses dois sistemas é dada, de modo simplificado, pela expressão matricial:

\(\begin{bmatrix}y \\ i \\ q \end{bmatrix} = \begin{bmatrix} 0,3 &2\beta &\gamma \\ 3\alpha &-\beta &-0,3 \\ \alpha &-0,5 & -3\gamma \end{bmatrix} \cdot \begin{bmatrix}r \\ g \\ b \end{bmatrix}\)

Sabendo que uma cor no sistema RGB descrita por (0,2; 0,5; 0,4) está associada a uma cor no sistema YIQ descrita por (0,4; –0,15; –0,33), determine α, β e γ.