(UNESP - 1 FASE)De um paraleleppedo reto-retngulo
(UNESP - 1ª FASE)
De um paralelepípedo reto-retângulo de dimensões 20 cm por \(6 \sqrt{2}\) cm por \(6 \sqrt{2}\) cm serão retirados dois cubos, cujos lados medem x cm. Esses cubos têm três arestas contidas em três arestas do paralelepípedo e uma das faces contida em uma mesma face quadrada do paralelepípedo.
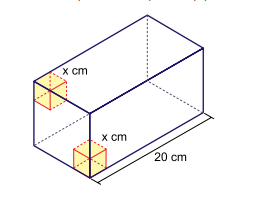
Ao adotar o valor máximo para x, o volume do prisma remanescente, após a retirada dos cubos, será igual a:
A
\(36(40-3\sqrt{2}) \ cm^{3}\)
B
\(108(10-\sqrt{2}) \ cm^{3}\)
C
\(30(9-\sqrt{3}) \ cm^{3}\)
D
\(36(10-3\sqrt{2}) \ cm^{3}\)
E
\(30(10-3\sqrt{2}) \ cm^{3}\)


