(AFA - 2014)Considere os grficos abaixo das funes
(AFA - 2014)
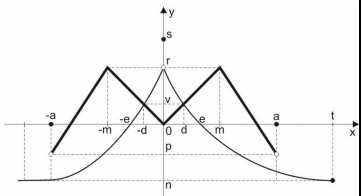
Considere os gráficos abaixo das funções reais \(f: A \rightarrow \mathbb{R}\) e \(g: B \rightarrow \mathbb{R}\).
Sabe-se que \(A= \left [ -a,a \right ]; B=\, ] -\infty,t]; g(-a)<f(-a); g(0)>f(0); g(a)\) e \(g(x)=n\) para todo \(x\leq -a\).
Analise as afirmativas abaixo e marque a FALSA.
A
A função f é par
B
se \(x\: \epsilon \: ]\: d,m\: [\) , então \(f(x)\cdot g(x)<0\)
C
\(Im(g)=[n,r[\: \cup\: \left \{ s \right \}\)
D
A função \(h:E\rightarrow \mathbb{R}\) dada por \(h(x)= \frac{-2}{\sqrt{f(x)-g(x)}}\) está definida se \(E = \left \{ x\: \epsilon \: \mathbb{R} \: | -a\: \leq x< \: -d\: \: \: ou\: \: \: d\: < x\leq \: a\right \}\)


