(FUVEST - 2023)Considere as circunferncias e a ret

(FUVEST - 2023)

Considere as circunferências \(C,C_{1},C_{2},C_{3},...,C_{n},...\) e a reta s satisfazendo as seguintes propriedades:

 

 

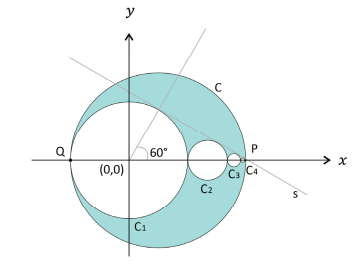
• A circunferência \(C_{1}\) tem centro (0,0) e raio \(r=4\). Os centros das demais circunferências pertencem ao eixo \(Ox\).

• A circunferência \(C_{2}\) é tangente a \(C_{1}\) e a \(C_{3}\), a circunferência \(C_{3}\) é tangente a \(C_{2}\) e a \(C_{4}\), e assim por diante.

• A reta s é tangente a cada circunferência \(C_{n}\) para \(n\geq 1\).

• O segmento que liga o centro de \(C_{1}\) ao ponto em que s tangencia \(C_{1}\) forma um ângulo de 60° com o eixo \(Ox\).

• A circunferência C é tangente a \(C_{1}\) no ponto \(Q = (-4,0)\) e passa pelo ponto \(P= (x_{0},0)\).

 

Com base nessas informações,

a) determine o raio da circunferência C.

b) dado \(n\geq 1\), determine a razão entre os raios das circunferências consecutivas \(C_{n+1}\) e \(C_{n}\).

c) determine a área da região sombreada na figura.