(FUVEST - 2023)Considere e a funo dada por .a) Det

(FUVEST - 2023)

Considere \(a,b,c \ \epsilon \mathbb{R}\) e a função \(f:\ \mathbb{R} \rightarrow \mathbb{R}\) dada por \(f(x)= ax^{2}+bx+c\).

 

a) Determine os valores de 𝑎, 𝑏 e 𝑐 para que 𝑓(1) = 1, 𝑓(0) = 0 e 𝑓(-1) = 1.

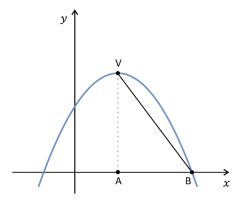
b) Para 𝑎 = -1 e 𝑏 = 4, determine o valor de 𝑐 de modo que a área do triângulo 𝐴𝐵𝑉 da figura seja igual a 32 u.a., onde 𝑉 é o vértice da parábola representada por 𝑓.

 

c) Considere \(g:\ \mathbb{R} \rightarrow \mathbb{R}\) a função dada por \(g(t)= cos \ t\). Se 𝑎 = 3 e 𝑐 = -8, determine para quais valores de 𝑏 a equação \(f(g(t)) = 0\) possui ao menos uma solução real.