(FUVEST - 2024)Matrizes podem ser usadas para se o
(FUVEST - 2024)
Matrizes podem ser usadas para se obter informações sobre uma rede social. Para compreender como isso pode ser feito, consideremos como exemplo uma pequena rede social formada por 4 pessoas: P1, P2, P3, P4. A matriz associada a essa rede social é a matriz 4×4:
\(M= \begin{pmatrix} 0 & 1 & 0 &1 \\ 0 & 0 & 1 &0 \\ 1 & 1 & 0&1 \\ 1 & 0 & 1 & 0 \end{pmatrix}\)
O valor 1 (um) na posição a32 (linha 3, coluna 2) da matriz significa que a pessoa P3 segue a pessoa P2, ao passo que o valor 0 (zero) na posição a24 (linha 2, coluna 4) significa que a pessoa P2 não segue a pessoa P4. O valor 0 (zero) será atribuído às posições aii. O significado do valor da posição bmn da matriz produto M x M=M2 é a quantidade de conexões da pessoa Pm até a pessoa Pn passando exatamente por uma pessoa, diferente delas duas, que chamaremos de conexão de grau 2.
Dessa forma, os valores das posições da matriz M2 podem refletir o alcance da rede social, suas potencialidades e fraquezas, a influência de certos membros dela, dentre outros aspectos.
Com relação à rede social apresentada, é correto afirmar que:
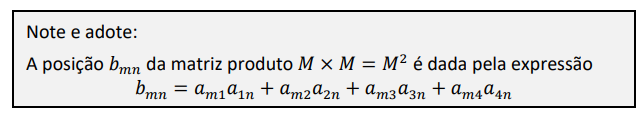
Existem 5 pares de pessoas diferentes (𝑃 ≠ 𝑃) que não possuem conexões de grau 2.
Existem 6 pares de pessoas diferentes (𝑃 ≠ 𝑃) que possuem apenas uma conexão de grau 2.
Existem 3 pares de pessoas diferentes (𝑃 ≠ 𝑃) que possuem 2 conexões de grau 2 diferentes.
Existem 3 pessoas que possuem conexões de grau 2 com todas as outras pessoas da rede social.
Existe apenas 1 pessoa 𝑃 (𝑖 ≠ 3) tal que 𝑃 e 𝑃ଷ seguem-se mutuamente.


