(Ita 1995) Sabendo-se que e são raízes do polinômi
Matemática | polinômios | equações polinomiais | interpretação geométrica das raízes de um polinômio
(Ita 1995) Sabendo-se qu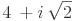e 
e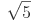 
são raízes do polinômio 2x5 - 22x4 + 74x3 + 2x2 - 420x + 540, então a soma dos quadrados de todas as raízes reais é:
A
17
B
19
C
21
D
23
E
25
