(ITA 1997) Seja A o ponto de intersecção das retas
Matemática | geometria analítica | teorema angular de retas | condição de paralelismo entre duas retas
Matemática | geometria analítica | teorema angular de retas | condição de perpendicularismo entre duas retas
Matemática | geometria analítica | teorema angular de retas | equação de uma reta passado por P(x,y)
(ITA 1997) Seja A o ponto de intersecção das retas r e s dadas, respectivamente, pelas equações x + y = 3 e x - y = -3. Sejam B e C pontos situados no primeiro quadrante com B ∈ r e C ∈ s. Sabendo que d(A, B) = d(A, C) =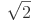 
, então a reta passando por B e C é dada pela equação
A
2x + 3y = 1
B
y = 1
C
y = 2
D
x = 1
E
x = 2
