(ITA - 2005 - 1 FASE )Considere uma rampa de ngulo
(ITA - 2005 - 1 FASE ) Considere uma rampa de ângulo θ com a horizontal sobre a qual desce um vagão, com aceleração a, em cujo teto está dependurada uma mola de comprimento l, de massa desprezível e constante de mola k, tendo uma massa m fixada na sua extremidade.
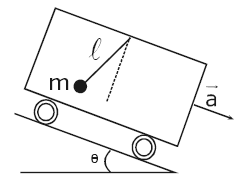
Considerando que l0 é o comprimento natural da mola e que o sistema está em repouso com relação ao vagão, pode-se dizer que a mola sofreu uma variação de comprimento Δl = l – l0 dado por:
A
\(\Delta l = mgsen\Theta lk\)
B
\(\Delta l = mgcos\Theta lk\)
C
\(\Delta l = \sqrt{a^{2} - 2agcos\Theta + g^{2}lk}\)
D
\(\Delta l = mglk\)
E
\(\Delta l = \sqrt{a^{2} - 2agsen\Theta + g^{2}lk}\)


