(UNESP 2021 - 1 fase)O mtodo matemtico a seguir ut
(UNESP 2021 - 1ª fase)
O método matemático a seguir é utilizado no cálculo por trilateração.
\(P = (u_x, u_y):\)
\((u_x - x_1)^2 + (u_y - y_1)^2 = {r_1}^2\), sendo \(M_1 (x_1, y_1)\)
\((u_x - x_2)^2 + (u_y - y_2)^2 = {r_2}^2\), sendo \(M_2 (x_2, y_2)\)
\((u_x - x_3)^2 + (u_y - y_3)^2 = {r_3}^2\), sendo \(M_3 (x_3, y_3)\)
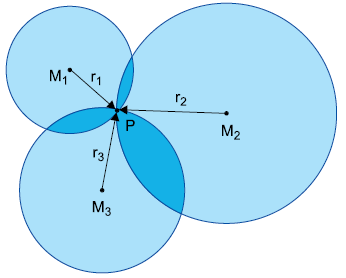
(Djonathan Krause. http://dsc.inf.furb.br. Adaptado.)
Esse cálculo permite
obter a área do setor circular a partir de um ângulo central, princípio do sensoriamento remoto.
localizar um ponto a partir de referências conhecidas, princípio do sistema de posicionamento global.
determinar a altitude de um ponto a partir de pontos de intersecção, princípio da hipsometria.
representar uma superfície plana a partir de uma superfície esférica, princípio das projeções cartográficas.
criar linhas imaginárias de meridianos e de paralelos a partir da distância entre os raios, princípio das coordenadas geográficas.


