(UNICAMP - 2022 - 2 fase)Recentemente, os arquelog

(UNICAMP - 2022 - 2ª fase)

Recentemente, os arqueólogos do Reino Unido apresentaram novas evidências sobre a origem do círculo de pedras de Stonehenge, na Grã-Bretanha. Testes geoquímicos indicam que a maioria dos monumentos megalíticos compartilham uma origem comum a cerca de vinte e cinco quilômetros de distância, enquanto as pedras azuis menores podem ter sido trazidas de outro monumento que foi desmontado e movido duzentos e oitenta quilômetros.

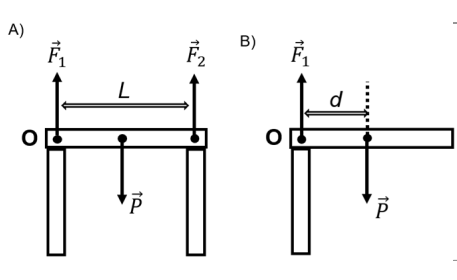
a) Observe o conjunto de pedras mostrado na figura A, e considere que a pedra na horizontal está em equilíbrio estático, sustentada pelas duas pedras verticais de mesma altura. A pedra horizontal é homogênea, estando a sua massa uniformemente distribuída ao longo do seu comprimento L = 4,0 m. A força vertical \(\vec {F_1}\) indicada na figura A tem módulo igual a \(F_1 = 9,0 \cdot 10^4N\). Suponha que uma das pedras verticais se rompa, gerando, imediatamente após a ruptura, o diagrama de forças mostrado na figura B. Na situação da figura A, a força peso – que age no centro de massa da pedra horizontal – produz um torque com módulo \(\tau _P\) em relação ao ponto O. O módulo do torque \(\tau _P\) é dado pelo produto do módulo da força peso P vezes a distância d do centro de massa ao ponto O. Calcule o módulo do torque resultante \(\tau _P\) na situação da figura B.

 

b) Um mistério que permanece sobre o monumento de Stonehenge diz respeito ao modo como pedras tão pesadas teriam sido deslocadas, percorrendo grandes distâncias. Para ilustrar tal desafio, calcule o trabalho que deve ser realizado por uma força horizontal aplicada a uma pedra de massa \(M = 1,8 \cdot 10^4 \ kg\) para arrastá-la, com velocidade constante, por uma distância d = 20 km em contato com uma superfície horizontal de coeficiente de atrito cinético igual a \(\mu _c = 0,6\) Sabendo que \(1 kWh = 3,6 \cdot 10^6 J\), expresse sua resposta em kWh.