(AFA - 2021 - Modelo C - Questo 30)Considere a fig
(AFA - 2021 - Modelo C - Questão 30)
Considere a figura a seguir.
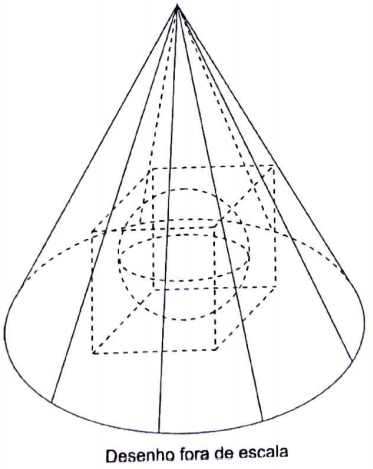
Nela está representada a inscrição de uma esfera num cubo que, por sua vez, está inscrito num cone equilátero, de tal forma que uma de suas faces está apoiada na base do cone e os vértices da face oposta estão na lateral do cone.
A projeção ortogonal do vértice do cone à sua base contém dois pontos de tangência da esfera com o cubo.
Se R e r são, respectivamente, as medidas do raio da base do cone e do raio da esfera, em cm, então
A
\(\frac{R}{r} = \frac{3 + 2 \sqrt3}{3}\)
B
\(\frac{r}{R} = \frac{3 \sqrt2 - 2 \sqrt3}{2}\)
C
\(\frac{R}{r} = \frac{2 \sqrt6 + 3 \sqrt2}{3}\)
D
\(\frac{r}{R} = \frac{2\sqrt6 - 3\sqrt2}{2}\)


