(Fgv 2010) Os pontos A(–1, 4), B(2, 3) e C não são
Matemática | geometria analítica | teorema angular de retas | condição de paralelismo entre duas retas
Matemática | geometria analítica | teorema angular de retas | condição de perpendicularismo entre duas retas
Matemática | geometria analítica | teorema angular de retas | equação de uma reta passado por P(x,y)
(Fgv 2010) Os pontos A(–1, 4), B(2, 3) e C não são colineares. O ponto C é tal que a área do triângulo ABC é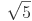 
. Nas condições dadas, o lugar geométrico das possibilidades de C é representado no plano cartesiano por um(a)
A
par de pontos distantes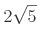 
um do outro.
B
reta perpendicular a AB que passa por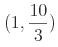 
.
C
reta perpendicular a AB que passa por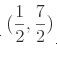 
.
D
par de retas paralelas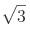 
distantes uma da outra.
E
par de retas paralelas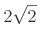 
distantes uma da outra.
