(FUVEST - 2002 - 2 FASE)Um astrnomo, ao estudar um

(FUVEST - 2002 - 2 FASE) 

Um astrônomo, ao estudar uma estrela dupla E₁-E₂, observou que ambas executavam um movimento em torno de um mesmo ponto P, como se estivessem ligadas por uma barra imaginária. Ele mediu a distância D entre elas e o período T de rotação das estrelas, obtendo T = 12 dias. Observou, ainda, que o raio R₁, da trajetória circular de E₁, era três vezes menor do que o raio R₂, da trajetória circular de E₂. Observando essas trajetórias, ele concluiu que as massas das estrelas eram tais que M₁ = 3 M₂. Além disso, supôs que E₁ e E₂ estivessem sujeitas apenas à força gravitacional entre elas.

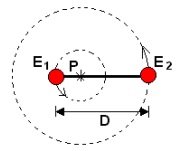
A partir das medidas e das considerações do astrônomo:

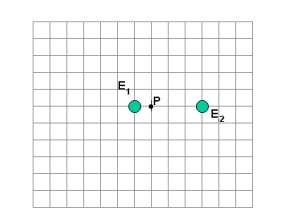
a) Indique as posições em que E₁ e E₂ estariam, quinze dias após uma observação em que as estrelas foram vistas, como está representado no esquema da folha de respostas. Marque e identifique claramente as novas posições de E₁ e E₂ no esquema da folha de respostas.

b) Determine a razão\(R = \frac{V_2}{V_1}\) entre os módulos das velocidades lineares das estrelas E₂ e E₁.

c) Escreva a expressão da massa M₁ da estrela E₁, em função de T, D e da constante universal da gravitação G.