(FUVEST - 2002 - 1a fase)A figura abaixo represent
(FUVEST - 2002 - 1a fase)
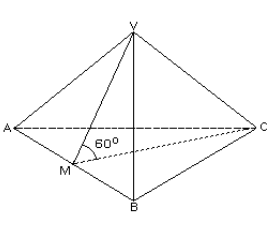
A figura abaixo representa uma pirâmide de base triangular ABC e vértice V. Sabe-se que ABC e ABV são triângulos equiláteros de lado \(l\) e que M é o ponto médio do segmento AB. Se a medida do ângulo \(V\hat{M}C\) é 60°, então o volume da pirâmide é:
A
\(\frac{\sqrt3}{4}l^3\)
B
\(\frac{\sqrt3}{8}l^3\)
C
\(\frac{\sqrt3}{12}l^3\)
D
\(\frac{\sqrt3}{16}l^3\)
E
\(\frac{\sqrt3}{18}l^3\)


