(FUVEST - 2002 - 1a fase)Na figura abaixo, o quadr
(FUVEST - 2002 - 1a fase)
Na figura abaixo, o quadrilátero ABCD está inscrito numa semi-circunferência de centro A e raio AB = AC = AD = R. A diagonal AC forma com os lados BC e AD ângulos α e β, respectivamente. Logo, a área do quadrilátero ABCD é:
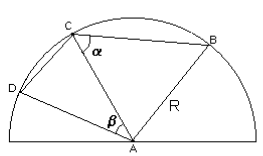
A
\(\frac{R^2}{2}(sen2\alpha+sen\beta)\)
B
\(\frac{R^2}{2}(sen\alpha+sen2\beta)\)
C
\(\frac{R^2}{2}(cos2\alpha+sen2\beta)\)
D
\(\frac{R^2}{2}(sen\alpha+cos\beta)\)
E
\(\frac{R^2}{2}(sen2\alpha+cos\beta)\)
