(FUVEST - 2017 - 2 FASE)Um caminho deve transporta

(FUVEST - 2017 - 2ª FASE)

Um caminhão deve transportar, em uma única viagem, dois materiais diferentes, \(X\) e \(Y\) , cujos volumes em m³ são denotados por \(x\) e \(y\), respectivamente. Sabe-se que todo o material transportado será vendido. A densidade desses materiais e o lucro por unidade de volume na venda de cada um deles são dados na tabela a seguir.

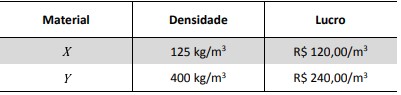
Para realizar esse transporte, as seguintes restrições são impostas:

I. o volume total máximo de material transportado deve ser de 50 m³ ;

II. a massa total máxima de material transportado deve ser de 10 toneladas.

Considerando essas restrições:

a) esboce, no plano cartesiano preparado na página de respostas, a região correspondente aos pares \((x,y)\) de volumes dos materiais \(X\) e \(Y\) que podem ser transportados pelo caminhão;

b) supondo que a quantidade transportada do material Y seja exatamente 10m³ , determine a quantidade de material \(X\) que deve ser transportada para que o lucro total seja máximo;

c) supondo que a quantidade total de material transportado seja de 36 m³ , determine o par \((x,y)\) que maximiza o lucro total.