(AFA - 2020)Em uma roda gigante, a altura h, em me

(AFA - 2020)

Em uma roda gigante, a altura h, em metros, em que uma pessoa se encontra, em relação ao solo, no instante, t, em segundo, é dada pela função \(h:\mathbb{R}\rightarrow\mathbb{R}\), definida por 

\(h(t)=a+B\sin(Ct)\)

, em que A, B e C são são constantes reais.

A figura a seguir ilustra o gráfico dessa função, no intervalo [0,150]

(figura)

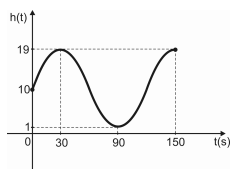
Analise cada proposição abaixo quanto a ser (V) verdadeira ou (F) Falsa

( ) \(|A\cdot B\cdot C|=\pi\)

( ) No instante t=20s, a pessoa estará a uma altura h tal que \(h\in[17,5;17,8]\)

( ) A função real f definida por \(f(t)=10-9\cos\left(\frac{3\pi}{2}-\frac{\pi}{60}t \right )\) é idêntica à função h

Sobre as proposições, tem-se que