(AFA - 2023)O grfico abaixo representa a funo real
(AFA - 2023)
O gráfico abaixo representa a função real \(f(x)= a + b \cdot e^{-x}\) , em que \(a\) e \(b \ \epsilon \ \mathbb{R}\), e é o número de Eüler e a reta tracejada é a assíntota ao gráfico de f.
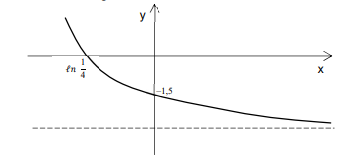
Considere que f é invertível e que ℓ𝑛 corresponde ao logaritmo na base e.
A função inversa de f, denotada por \(f^{-1}\) , é
A
\(f^{-1}(x)= -ln (2x+4)\)
B
\(f^{-1}(x)= ln (x+4)^{-1}\)
C
\(f^{-1}(x)= -ln (-2x+4)\)
D
\(f^{-1}(x)= ln (-x+4)^{-1}\)


