(IME - 2008/2009)Considere o sistema acima, onde u
(IME - 2008/2009)
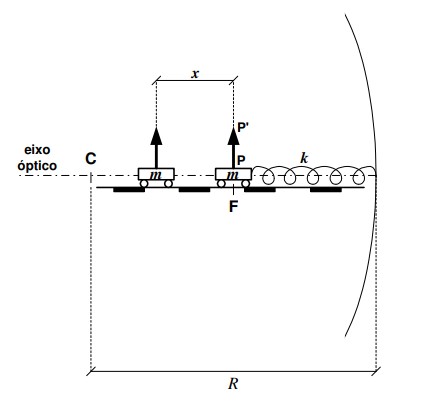
Considere o sistema acima, onde um objeto PP’ é colocado sobre um carrinho de massa m que se move, em movimento harmônico simples e sem atrito, ao longo do eixo óptico de um espelho esférico côncavo de raio de curvatura R. Este carrinho está preso a uma mola de constante k fixada ao centro do espelho, ficando a mola relaxada quando o objeto passa pelo foco do espelho. Sendo x a distância entre o centro do carrinho e o foco F, as expressões da frequência w de inversão entre imagem real e virtual e do aumento M do objeto são
\(w = \sqrt{\frac{k}{m}} \ e \ M = -\frac{R}{2x}\)
\(w = \sqrt{\frac{m}{k}} \ e \ M = -\frac{R(R+2x)}{4x(\frac{R}{2} + x)}\)
\(w = \sqrt{\frac{k}{m}} \ e \ M = -\frac{R(R+x)}{4x(\frac{R}{2} + x)}\)
\(w = \sqrt{\frac{k}{R}} \ e \ M = -\frac{2x}{R}\)
\(w = \sqrt{\frac{k}{m}} \ e \ M = -\frac{R(R+2x)}{4x(\frac{R}{2} - x)}\)


