(UFU - 2017 - 1 FASE)Um designer de jogos virtuais

(UFU - 2017 - 1ª FASE)

Um designer de jogos virtuais está simulando alguns deslocamentos associados com uma pirâmide quadrangular regular, em que o lado do quadrado da base mede 40 cm.

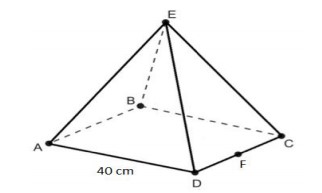
(Figura ilustrativa e sem escalas)

Ele simula a trajetória de um lagarto pelas faces da pirâmide. Inicialmente o lagarto desloca-se de A até E e, posteriormente, de E até F, em que F é o ponto médio de CD. Cada um desses dois trechos da trajetória ocorre em linha reta.

A projeção perpendicular dessa trajetória em ABCD, presente no plano da base da pirâmide, descreve uma curva R, a qual é a união de dois segmentos.

Nessas condições, o comprimento de R, em cm, é igual a