(UNESP - 2024)A figura indica uma roleta circular,

(UNESP - 2024)

A figura indica uma roleta circular, dividida em cinco setores. As posições finais do ponteiro giratório da roleta, após um giro aleatório em torno do centro do círculo, possuem mesmas probabilidades. Se, após o giro, o ponteiro para sobre a linha compartilhada por setores circulares contíguos, ele é girado novamente.

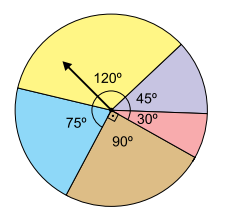
a) Girando-se ao acaso o ponteiro da roleta até que ele pare em uma região do interior de algum dos cinco setores, qual a probabilidade de que o ângulo central do setor seja obtuso? E qual a probabilidade de que esse ângulo seja agudo?

b) Girando-se ao acaso duas vezes o ponteiro da roleta e anotando-se os dois ângulos obtidos, qual é a probabilidade de que ao menos um deles seja ângulo interno de um polígono regular?