(UNICAMP - 2023- 2 fase)Na natureza, observa-se qu

(UNICAMP - 2023 - 2ª fase)

 

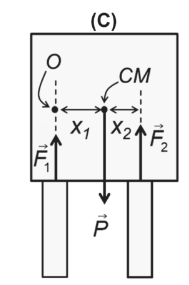
Na natureza, observa-se que a razão entre o diâmetro dos membros de sustentação de um animal e a sua altura é tanto menor quanto menor for o animal (ver figura A). Todavia, os diminutos seres humanos descritos no livro “Viagens de Gulliver” (Jonathan Swift, 1726) e no filme “Downsizing” (2017) têm essa razão mantida, diferentemente do que ocorre na natureza. Para ilustrar o comportamento da natureza, vamos tratar um caso simples: duas caixas cúbicas de água, uma grande – com lado $S = 4,0 \ m$ e massa $M= 6,4 \cdot 10^{4} \ kg$ –, e outra pequena – com lados $s= S/4= 1,0 \ m$ e massa $m= 1,0 \cdot 10^{3} \ kg$.

 

 

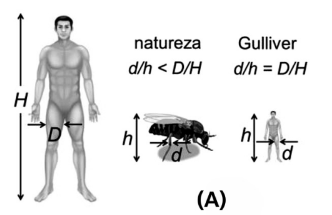
a) Suponha que cada caixa esteja em equilíbrio estático e seja sustentada por uma coluna de seção reta quadrada, centrada no fundo, conforme a figura B. Os lados das colunas são $D = 0,4\ m$ (caixa grande) e d (caixa pequena). Qual deve ser o tamanho d dos lados da coluna da caixa pequena para que a pressão exercida sobre essa coluna seja igual à pressão exercida pela caixa grande sobre a sua própria coluna?

 

 

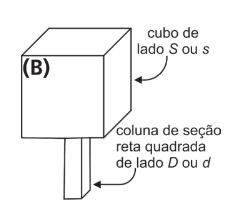
b) Vamos supor agora que o equilíbrio estático da caixa grande seja garantido por duas colunas de sustentação. As forças atuando na caixa são: o peso $\overrightarrow{P}$, no centro de massa CM, e as forças $\overrightarrow{F_{1}}$ e $\overrightarrow{F_{2}}$ exercidas pelas colunas. As linhas (tracejadas) de atuação das três forças estão contidas no plano vertical mostrado na figura C (no espaço de respostas). O módulo do torque resultante sobre a caixa, em relação ao ponto O, é dado por: $\left | \overrightarrow{\tau_{0}} \right | = \left | \overrightarrow{P} \right |x_{1}- \left | \overrightarrow{F_{2}} \right |(x_{1}+x_{2})$, sendo $x_1 = 1,8 \ m$ e $x_2 = 0,6 \ m$. Calcule os módulos das forças $\overrightarrow{F_{1}}$ e $\overrightarrow{F_{2}}$.