(UNICAMP - 2024)Use os valores aproximados: e .Tex

(UNICAMP - 2024)

Use os valores aproximados: \(g = 10 \ m/s^{2}\) e \(\pi=3\).

Texto comum às questões 26, 27, 28 e 29.

 

Uma das etapas mais difíceis de um voo espacial tripulado é a reentrada na atmosfera terrestre. Ao reencontrar as camadas mais altas da atmosfera, a nave sofre forte desaceleração e sua temperatura externa atinge milhares de graus Celsius. Caso a reentrada não ocorra dentro das condições apropriadas, há risco de graves danos à nave, inclusive de explosão, e até mesmo risco de ela ser lançada de volta ao espaço.

 

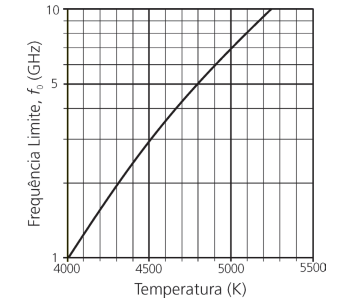
A temperatura extremamente elevada no exterior da cápsula ioniza o ar atmosférico à sua volta. Esses íons blindam a cápsula como uma gaiola de Faraday, impedindo, por alguns minutos, a comunicação por ondas eletromagnéticas de rádio (conversas entre a tripulação e a base na Terra, comandos à distância para ajustes de navegação, etc.). O gráfico da figura a seguir mostra que, quanto maior a temperatura do ar externo, T_ar, maior é a frequência limite da onda eletromagnética, f₀ , abaixo da qual não se pode estabelecer comunicação com a cápsula. Se a temperatura do ar for T_ar = 4800 K, qual é o comprimento de onda \(\lambda _{0}\) correspondente à frequência limite f₀?

 

Dado: Velocidade da luz no vácuo: \(c = 3,0 \times 10^{8} m/s\).