(FUVEST 2014 - 2 FASE) Um corpo de massa M desliza

(FUVEST 2014 - 2ª FASE) Um corpo de massa M desliza sem atrito, sujeito a uma força gravitacional vertical uniforme, sobre um "escorregador logarítmico": suas coordenadas (x, y) no plano cartesiano, que representam distâncias medidas em metros, pertencem ao gráfico da função \(f(x) = log_{\frac{1}{2}}x +4\).

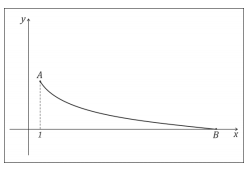
O corpo começa sua trajetória, em repouso, no ponto A, de abscissa x =1, e atinge o chão no ponto B, de ordenada y = 0, conforme figura ao lado. Não levando em conta as dimensões do corpo e adotando 10 m/s² como o valor da aceleração da gravidade, 

a) encontre a abscissa do ponto B;

b) escreva uma expressão para a energia mecânica do corpo em termos de sua massa M, de sua altura y e de sua velocidade escalar v;

c) obtenha a velocidade escalar v como função da abscissa do ponto ocupado pelo corpo;

d) encontre a abscissa do ponto a partir do qual b é maior do que \(\sqrt{60}\ m/s\).