(IME - 2020 - Questo 18)Quatro partculas, denomina
(IME - 2020 - Questão 18)
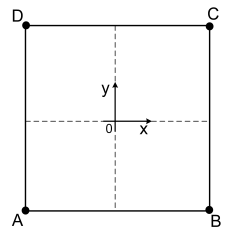
Quatro partículas, denominadas A, B, C e D, partem simultaneamente dos vértices de um quadrado de lado unitário. Todas as partículas apresentam velocidades escalares iguais durante suas trajetórias. A partícula A persegue a partícula B, de tal forma que o seu vetor velocidade está sempre na direção e sentido de A para B. O mesmo ocorre entre as partículas B e C, C e D e, finalmente, entre D e A. Tomando o centro do quadrado como origem do sistema de coordenadas, a tangente do angulo entre vetor unitário do sentido positivo do eixo x e o vetor que une o ponto A ao ponto B, quando A se encontra em um ponto arbitrário (x,y) da sua trajetória, é dada por:
\(\frac{x-y}{2x-2y+1}\)
\(\frac{1+x-y}{x+y}\)
\(-\frac{x-y}{x+y}\)
\(\frac{x}{y}-\frac{y}{x}\)
\(\frac{1+x+y}{1-x+y}\)


