(UFPR - 2022- 1 fase)Na figura ao lado, temos uma

(UFPR - 2022- 1ª fase)

 

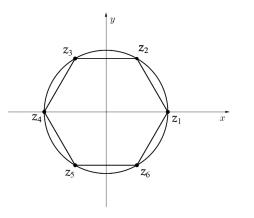
Na figura ao lado, temos uma circunferência de raio \(r< 0\) com centro na origem do plano complexo e, ao longo da circunferência, temos 6 números complexos: \(z_{1}, z_{2},z_{3},z_{4},z_{5},z_{6}\).  Supondo que os 6 números complexos são vértices de um hexágono regular e que \(z_{1}\) está no eixo x, considere as seguintes equações:

 

\(1.\ z_{2} + z_{6}= r^{2}\)

\(2.\ \overline{z_{3}}= z_{5}\)

\(3.\ z_{2} \cdot z_{3} = z_{4}\)

\(4.\ \frac{z_{5}}{z_{6}}= \frac{z_{6}}{r}\)

 

 

Assinale a alternativa correta.